三度同じ三角形になるはずだ。1組の辺とその両端の角が等しければ、合同。 これらの合同条件は、完全に暗記する必要がある。これから扱う合同の証明などで使用するので、まずは合同条件の暗記が絶対だ。 合同の記号は≡だ。 abc≡ defのように使う。三角形の合同条件 私は現在高一なんですが、三角形の合同条件に少し疑問があります。三角形の合同条件といえば、 ・3辺が全て等しい ・2辺とその挟む角が等しい ・1辺とその両端の角が等しい ですけど、この2つ目と3つめに疑問があるんです。こんにちは、ウチダショウマです。 今日は、中学2年生で習う 「直角三角形の合同条件」 について、まず「そもそもなぜ成り立つのか」を考察し、次に直角三角形の合同条件を使った証明問題を解説していきます。 直角三角形の合同条件2つ まず、一般的な三角形における合同条件3つについて

中2数学 チョー便利な直角三角形の2つの合同条件 Qikeru 学びを楽しくわかりやすく
三角形 合同 条件
三角形 合同 条件-三角形の合同条件と相似条件を3つの種類にまとめてみた 三角形の合同条件と相似条件をうまく覚えるために、3つの種類に分類してみたよ。 3つの何かが等しい条件 2つの角が等しい条件 2つの辺を角が挟んでいる条件 3つの何かが等しい条件 2つの角が等しい条件 2辺を角で挟んだ条件 合同条件4.両意の合同 今回は,前回扱った直角三角形の合同条件のうち, 斜辺と他の1辺がそれぞれ等しい を別の角度から眺めてみましょう. 具体的に書くと, abcと defで ∠c=∠f=90° ab=de ac=df
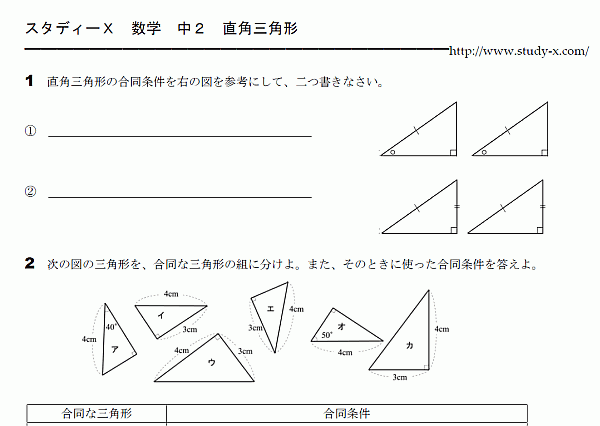


中2 数学 無料学習プリント教材
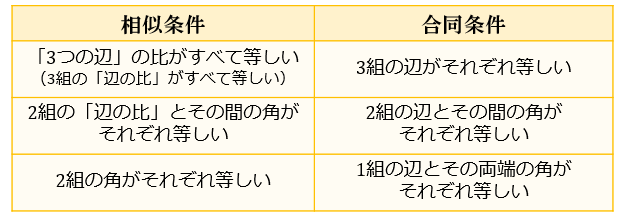
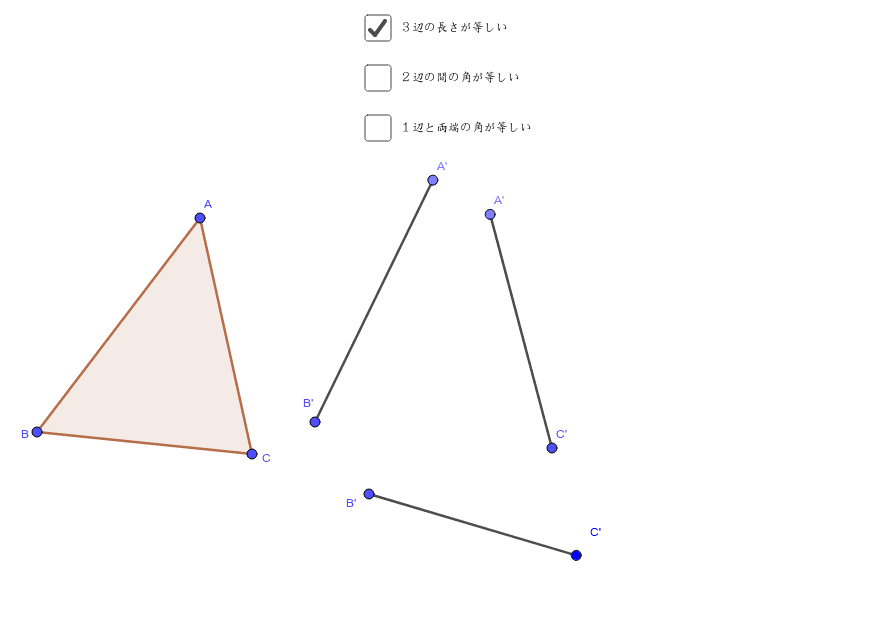
合同だとわかると 同じ三角形であるのですべてが等しい 相似条件 3辺の比が等しい;三角形の合同条件 チェックボックスで合同条件を1つ選びます。次に点a, b, cを動かすと合同条件に応じて点a', b', c'も変わります。現れたa', b', c'や辺、角の大きさを見て、 a'b'c'を abcと合同にできそうか考えてみましょう。なお点a', b', c'を動かして、点の位置や辺の向きなどを変えることもでき三角形の合同条件に関する史的考察 中 西 正 治 (羽曳野市立峰塚中学校) (1996年2月28日受付) 概 要昭和44年度の学習指導要領にもとづく教科書以後,三角形の合同条件は単に事実として記述さ れているのみで,その証明はほとんど示されてない。
二等辺三角形の性質/二等辺三角形になることを証明:角/三角形の合同利用/ 二等辺三角形の計算問題 /正三角形などの証明問題/正三角形などの計算問題/ 直角三角形の合同条件/ 直角三角形と二等辺三角形/垂線をひく/2 つの内角の和=90°直角三角形の合同条件が使えるのは 斜辺が等しいことが分かっているときだけ なので注意しておきましょう! 直角三角形の合同証明の書き方とは 直角三角形の合同条件を利用した、合同証明の問題に挑戦してみましょう。 二等辺三角形の形中2の直角三角形の合同条件のところです 学年 中学2年生, 単元 三角形, キーワード 数学,中2,直角三角形の合同条件,math
三角形の合同条件について,厳密性にこだわりましょう.厳密に証明するには, 使ってよい性質を明確にする必要があります. ユークリッド原論では三角形の合同の定理1,2,3をどのように証明 しているかを紹介します.こんにちは、ウチダショウマです。 今日は、中学2年生で習う 「直角三角形の合同条件」 について、まず「そもそもなぜ成り立つのか」を考察し、次に直角三角形の合同条件を使った証明問題を解説していきます。 直角三角形の合同条件2つ まず、一般的な三角形における合同条件3つについて三角形の合同条件 チェックボックスで合同条件を1つ選びます。次に点a, b, cを動かすと合同条件に応じて点a', b', c'も変わります。現れたa', b', c'や辺、角の大きさを見て、 a'b'c'を abcと合同にできそうか考えてみましょう。なお点a', b', c'を動かして、点の位置や辺の向きなどを変えることもでき


Studydoctor三角形の合同条件 中2数学 Studydoctor


三角形の 合同条件 相似条件 の意味について 三角比や正弦定理 余弦定理の理解も深くなる ここからはじめる高校数学
冴場:この場合、三角形の合同条件を使って注文すれば、同じ三角形のイヤリングができるはずよ。 数未 :明奈さんの注文の仕方は 「2つの辺の〇二等辺三角形の性質を,どのように利用したか? 〇合同条件が,なぜ,2つだけなのか? こうした学習により,「 証明する力 」を一層伸ばすことができます。つまり,「直角三角形の合同条件を,どこで,どのように,利用するか!2組の角度が等しい 相似だとわかると 対応する線分の比が等しい;
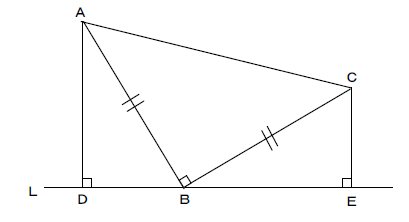


中2数学 直角三角形の合同証明のポイントと練習問題 やすひこ先生の中学生授業log


相似三角形定理 三角形相似 证明三角形相似 相似三角形性质
三角形 合同条件 2 つの三角形を移動して重ねあわせることができるとき、この 2 つの三角形は合同である。ここでいう移動とは、平行移動、回転移動、対称移動を組み合わせたものである。ある 2 つの三角形について、三度同じ三角形になるはずだ。1組の辺とその両端の角が等しければ、合同。 これらの合同条件は、完全に暗記する必要がある。これから扱う合同の証明などで使用するので、まずは合同条件の暗記が絶対だ。 合同の記号は≡だ。 abc≡ defのように使う。三角形 合同条件 2 つの三角形を移動して重ねあわせることができるとき、この 2 つの三角形は合同である。ここでいう移動とは、平行移動、回転移動、対称移動を組み合わせたものである。ある 2 つの三角形について、
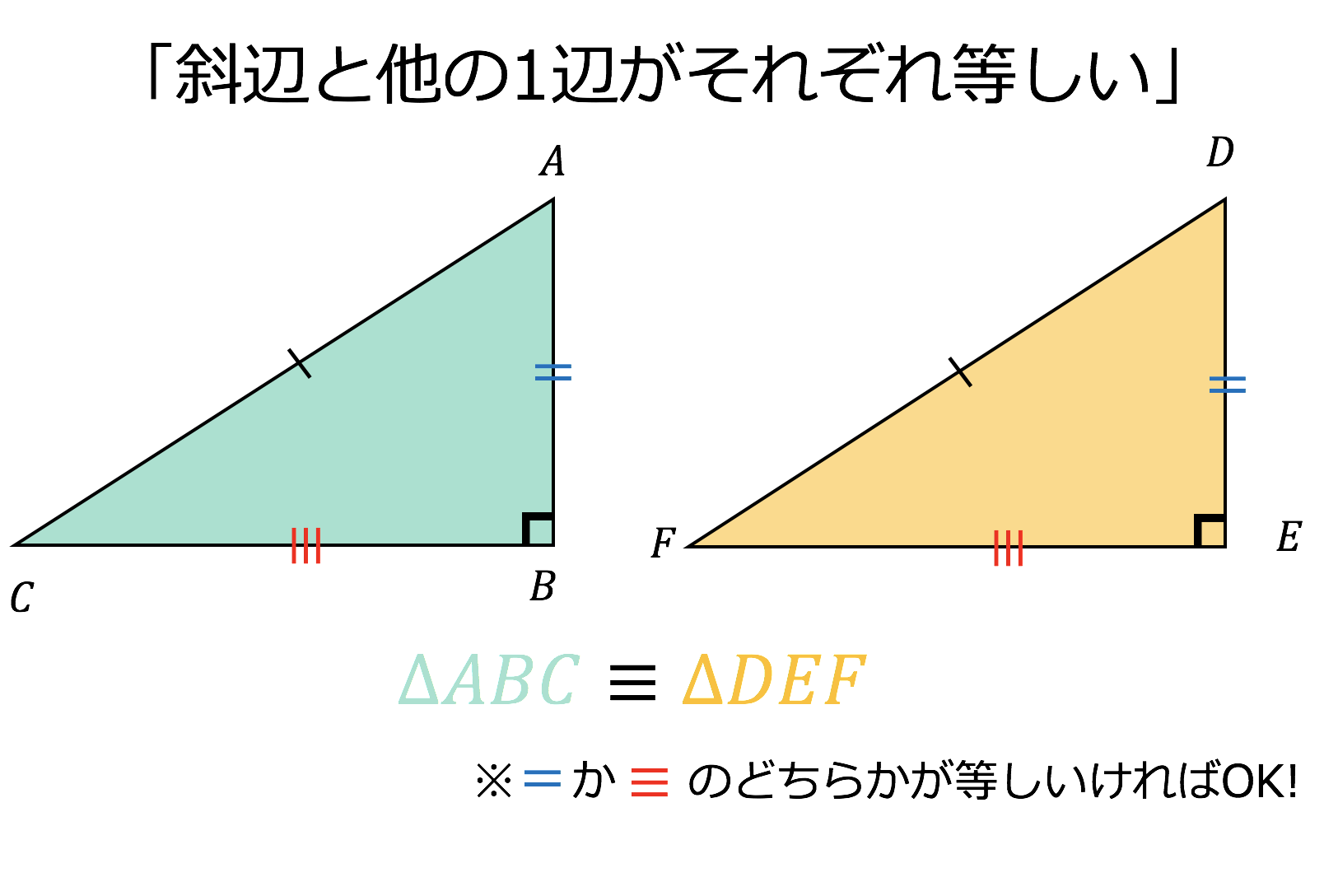


3分で分かる 三角形 直角三角形の合同条件とその使い方をわかりやすく 合格サプリ



直角三角形の合同条件 算数 数学が好きになりmath
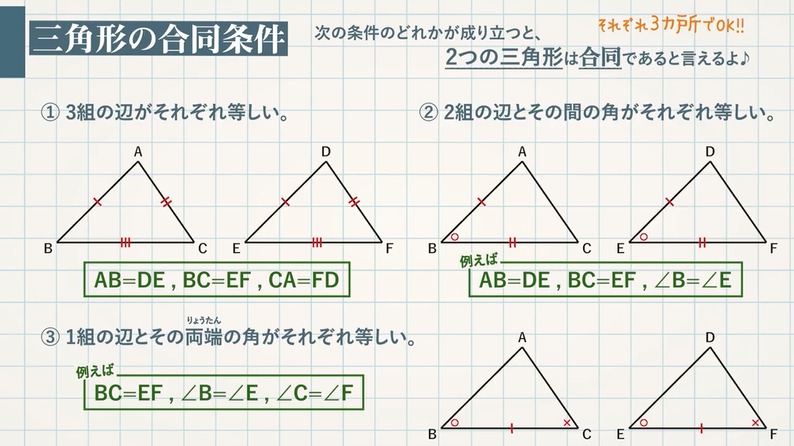
11三角形の合同条件を覚えられない ズバリ、三角形の合同条件をよく見てみよう。 これじゃ、答えになってない? 何かと同じではない? 三角形の合同条件は 1.三辺の長さが同じ 2.二辺の長さとそれらのはさむ角度が同じ三角形の合同条件とは? さて、合同な三角形は3つの角と3つの辺が等しくなっているという性質があることが分かりました。 では逆に、2つの三角形が合同であると示すためには、その3つの角と3つの辺を全て分かっている必要があるのでしょうか? 実は、そうではないのです。三角形の合同条件 三角形の合同条件 とは、 2つの三角形が合同であることを示すための条件 です。 以下の3つの合同条件のうち、どれかが成り立つ場合、その三角形は合同であるといえます。 3組の辺がそれぞれ等しい。 2組の辺とその間の角がそれぞれ等しい。 1組の辺とその両端の角がそれぞれ等しい。 直角三角形の合同条件は、次の2つです。 斜辺と1つの
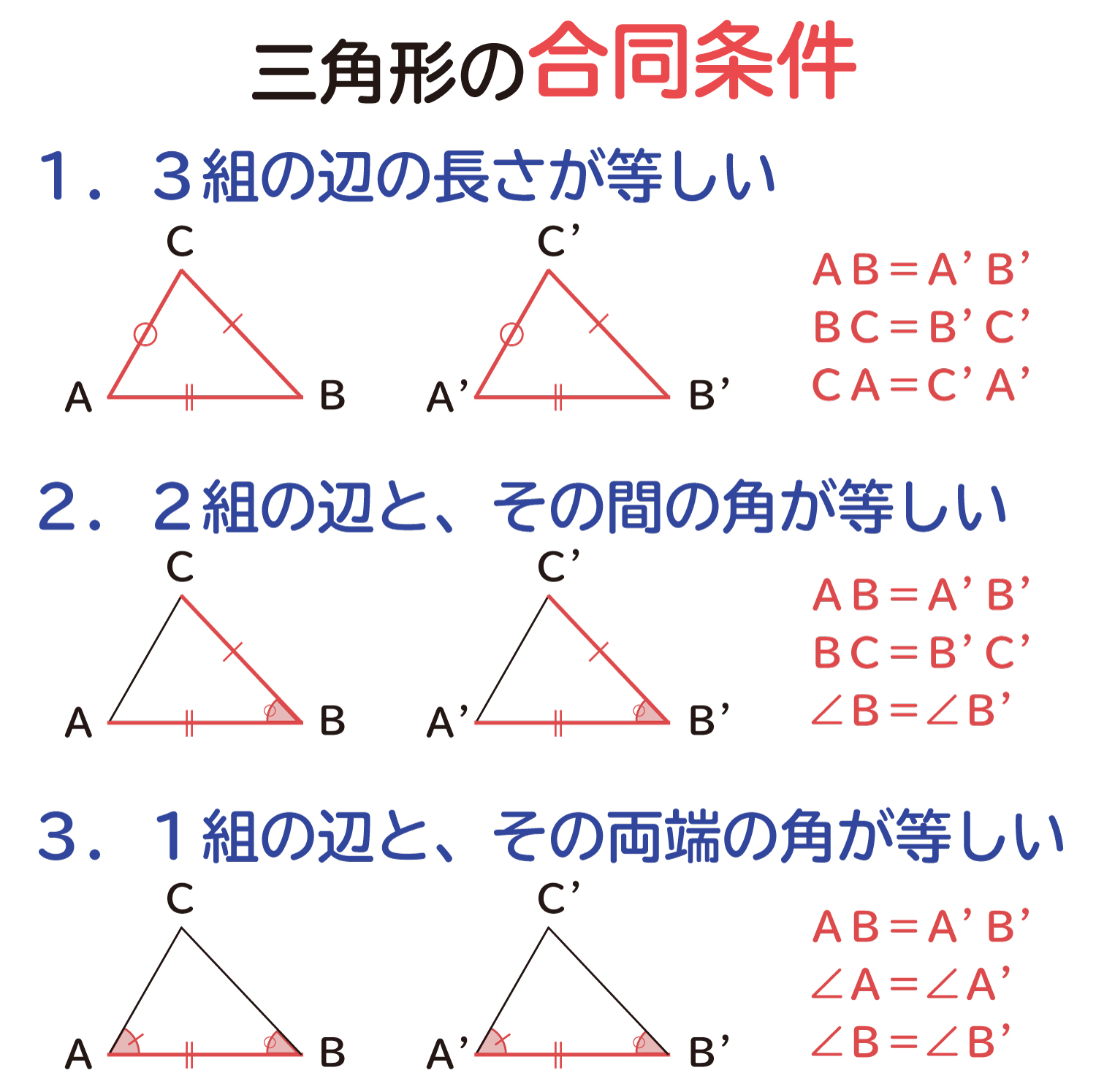


三角形の合同条件の説明 おかわりドリル



工程建设招标设标合同条件 第1部分 Word模板下载 招标 熊猫办公
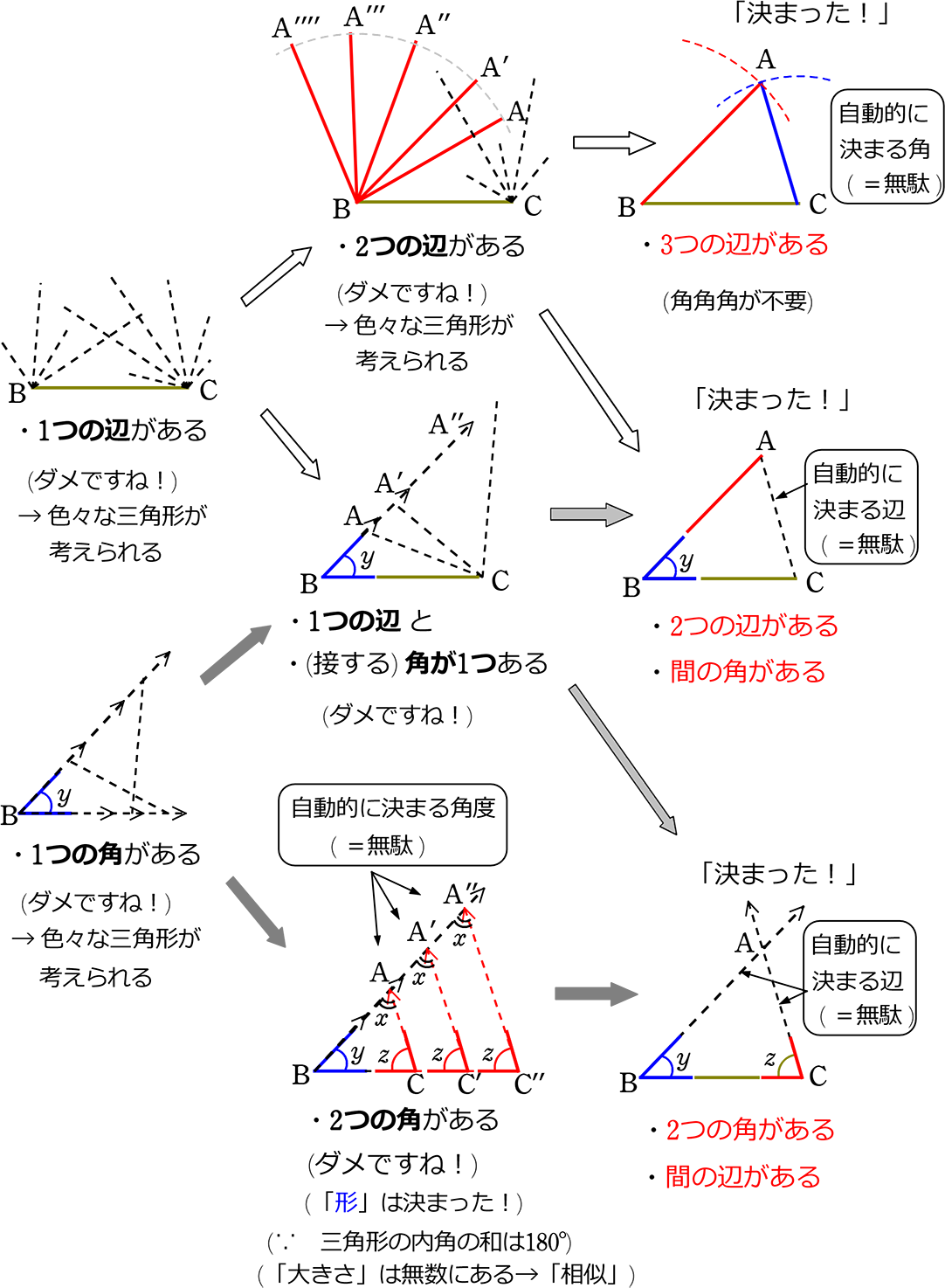
三角形の合同条件に関する史的考察 中 西 正 治 (羽曳野市立峰塚中学校) (1996年2月28日受付) 概 要昭和44年度の学習指導要領にもとづく教科書以後,三角形の合同条件は単に事実として記述さ れているのみで,その証明はほとんど示されてない。合同条件を満たすとなぜ合同なのか?を考えてみる まずは、三角形の合同条件についての復習 まずは、"合同"についての復習です。 "合同"とは、簡単に言えば、2つの図形を比べたとき、形と大きさが同じであることをいいます。 言い換えると、一方の図形を動かしたり裏返したりすると1つの辺の長さとその両端の角の大きさが決まると、三角形は1通りに決まるので、この条件を満たせば、2つの三角形は合同です。 3つの合同条件に共通することは、 辺と角を合わせて3か所が等しい ということです。
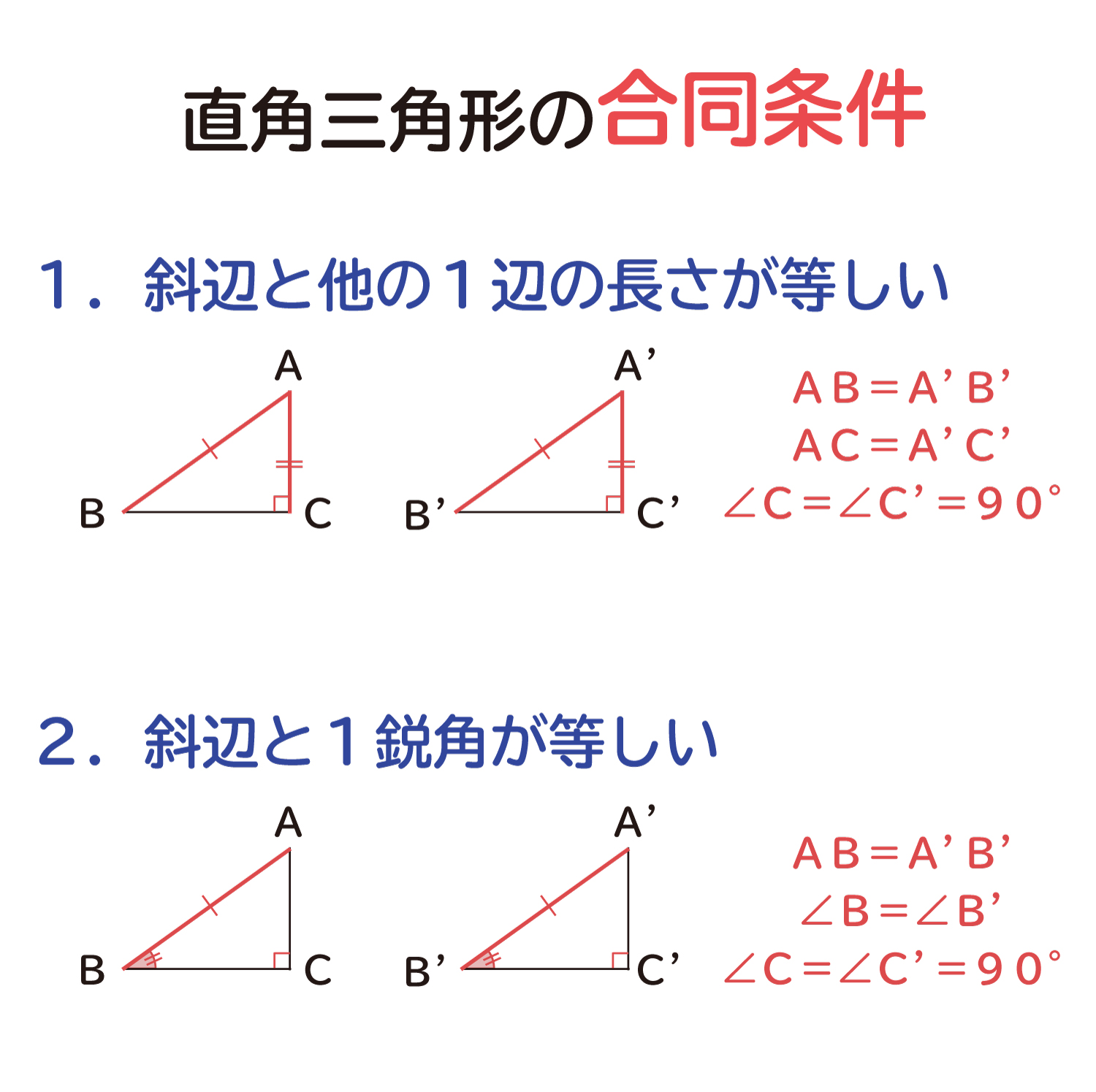


直角三角形の合同条件の説明 おかわりドリル


オリゲー15 合同条件ジャンゲーム 遊学塾 興味津々
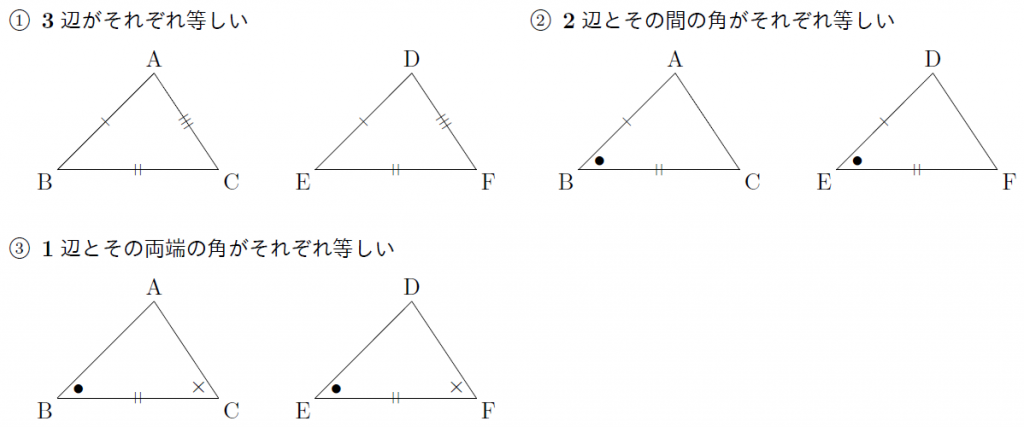
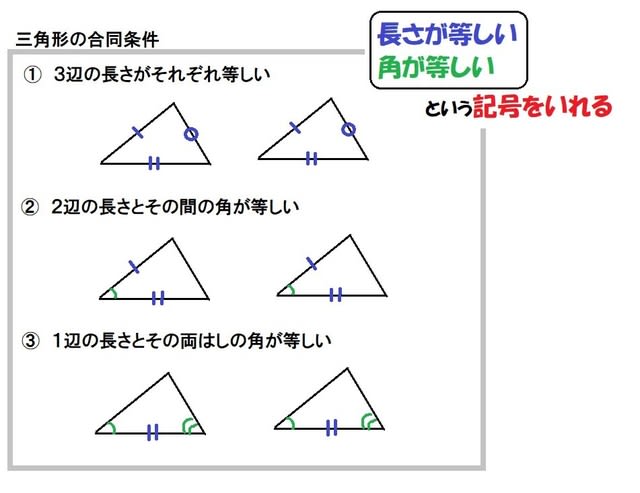
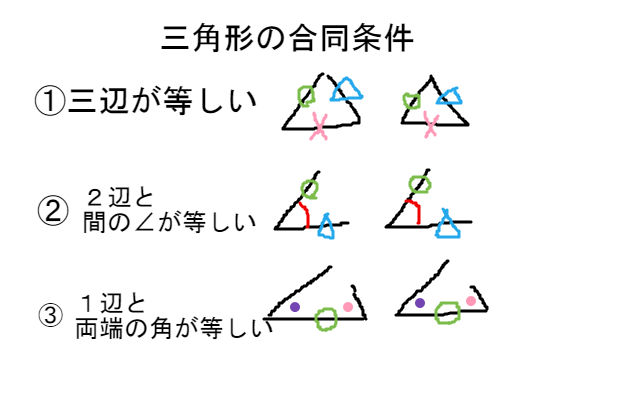
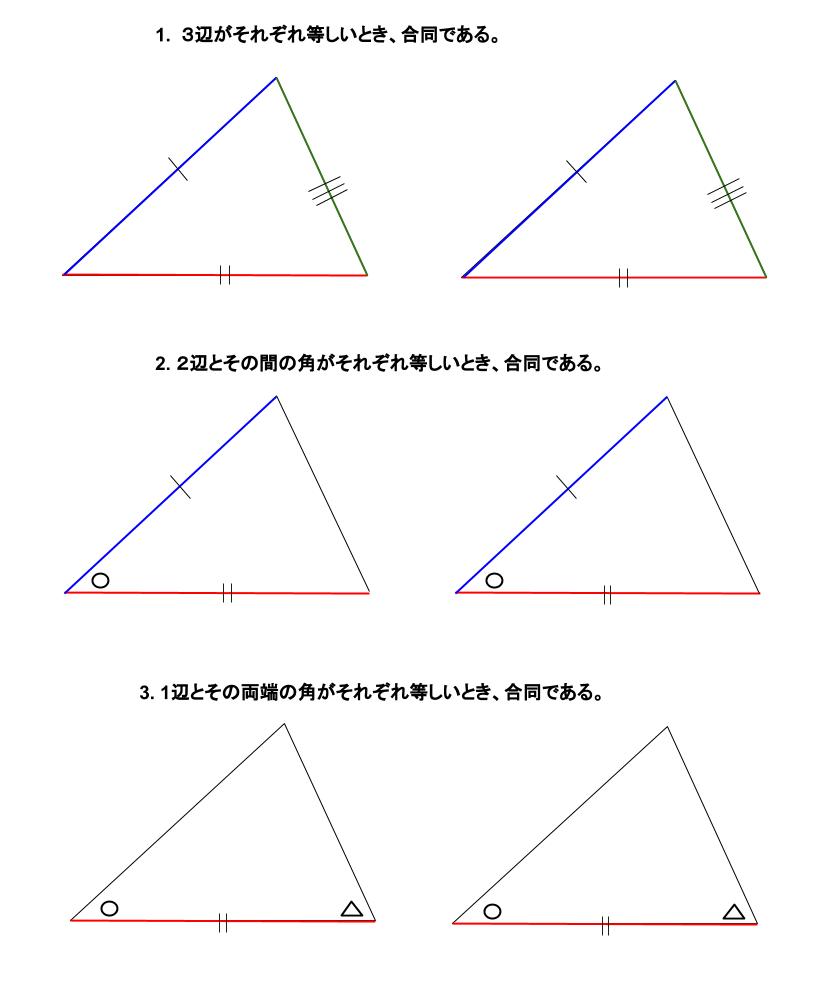
次の条件のどれかが成り立つと、$2$ つの三角形は合同であるといえます。 三角形の合同条件 ① $\textcolor{blue}{3}$ 組の辺がそれぞれ等しい。 ② $\textcolor{blue}{2}$ 組の辺とその間の角がそれぞれ等しい。 ③ $\textcolor{blue}{1}$ 組の辺とその両端の角がそれぞれ等しい。台形の合同条件 三角形の合同条件 三角形の合同条件 合同とは 一方の図形を移動させて他方に重ね合わせることができる場合、この2つの図形は 合同 であるという。 三角形の合同を判断する場合、重ねあわせなくても下記の3つの合同条件のうちどれか一つに当てはまれば合同だといえる 某所三角形の合同条件といえば・・・ ①3つの辺がそれぞれ等しい ②2つの辺とその間の角がそれぞれ等しい ③1つの辺とその両端の角がそれぞれ等しい この3つが、いわゆる合同条件です。 小学校5年生では、次のように学習します。


直角三角形の合同条件 On Vimeo
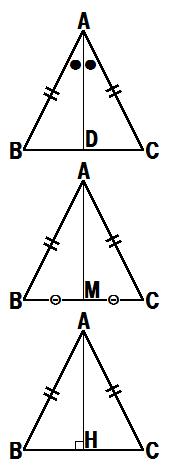


三角形の合同条件と二等辺三角形の底角 2 算数 数学記事
三角形の合同条件といえば・・・ ①3つの辺がそれぞれ等しい ②2つの辺とその間の角がそれぞれ等しい ③1つの辺とその両端の角がそれぞれ等しい この3つが、いわゆる合同条件です。 小学校5年生では、次のように学習します。中2の直角三角形の合同条件のところです 学年 中学2年生, 単元 三角形, キーワード 数学,中2,直角三角形の合同条件,math三角形の合同条件 現在 「二組の辺とその間にある角がそれぞれ等しい」 (一字一句間違えたらダメ。「二組」が「2組」でもアウト」 過去 「二辺夾角相等」 英語 「SAS」(side angle sideのこと)



直角三角形の合同条件を使った証明問題の解き方 現役塾講師のわかりやすい中学数学の解き方
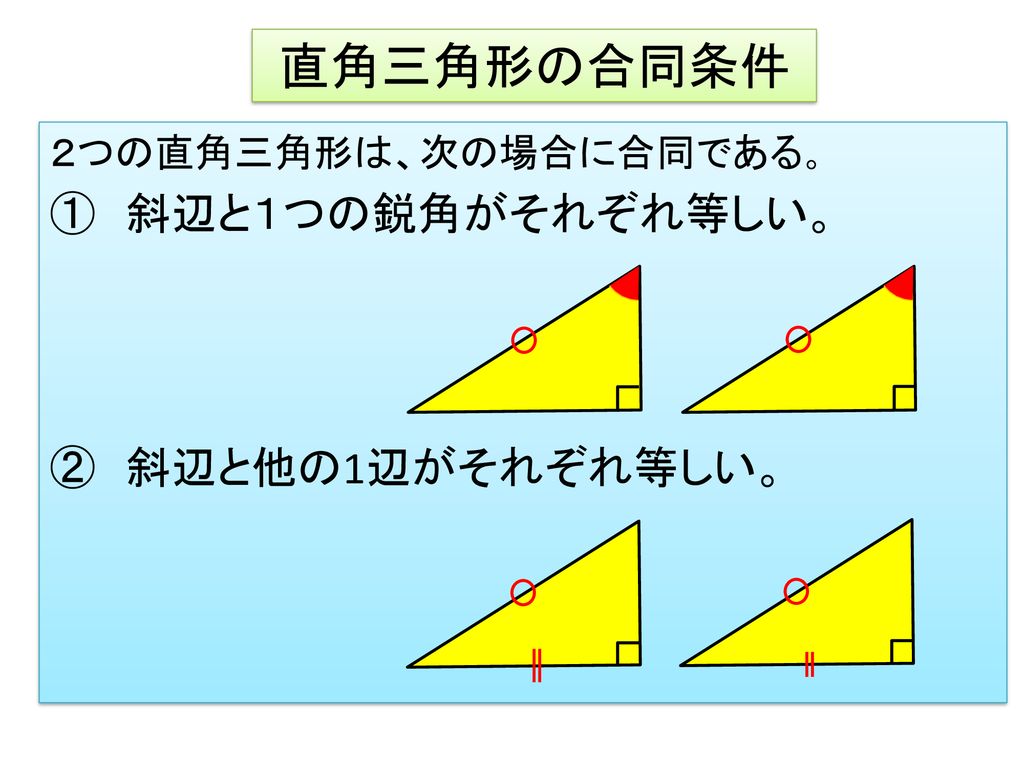


本時のねらい 直角三角形の合同条件を導き それを理解し 証明ができるようにする Ppt Download
三角形の合同条件 私は現在高一なんですが、三角形の合同条件に少し疑問があります。三角形の合同条件といえば、 ・3辺が全て等しい ・2辺とその挟む角が等しい ・1辺とその両端の角が等しい ですけど、この2つ目と3つめに疑問があるんです。三角形 合同条件 2 つの三角形を移動して重ねあわせることができるとき、この 2 つの三角形は合同である。ここでいう移動とは、平行移動、回転移動、対称移動を組み合わせたものである。ある 2 つの三角形について、それが 『三角形の合同条件』 というものです。 それぞれの三角形の長さや角の大きさを比較して 次の3つのいずれかの条件を満たせば 2つの三角形は合同だということがわかります。 3組の辺がそれぞれ等しい
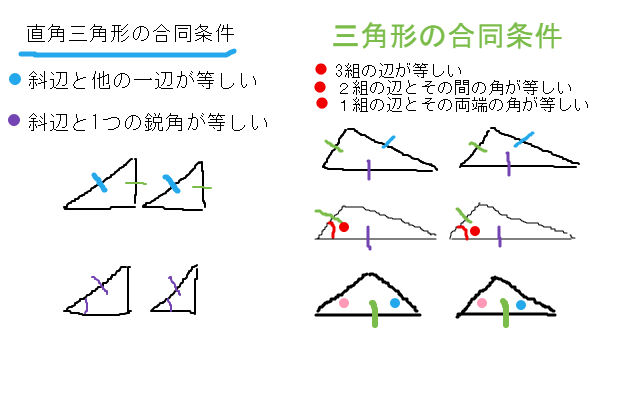


三角形 合同 相似条件 直角三角形の合同条件 中学数学 理科 寺子屋塾の復習サイト



数学 三角形の合同条件 定義 定理 Youtube
台形の合同条件 三角形の合同条件 三角形の合同条件 合同とは 一方の図形を移動させて他方に重ね合わせることができる場合、この2つの図形は 合同 であるという。 三角形の合同を判断する場合、重ねあわせなくても下記の3つの合同条件のうちどれか一つに当てはまれば合同だといえる 某所三角形の合同条件3つ超重要 それではいよいよ、「三角形の合同条件」について具体的に考えていきます。 といっても、$3$ つしかないため、覚えるのは比較的楽だとは思います。 3組の辺がそれぞれ等しい。 2組の辺とその間の角がそれぞれ等しい。三角形 合同条件 2 つの三角形を移動して重ねあわせることができるとき、この 2 つの三角形は合同である。ここでいう移動とは、平行移動、回転移動、対称移動を組み合わせたものである。ある 2 つの三角形について、



三角形の相似条件が見やすい図で一発理解できる 練習問題付き 高校生向け受験応援メディア 受験のミカタ


三角形の合同条件 まいにち一題 中学受験過去問題研究



三角形の合同条件


受験数学かずスクール 三角形の合同条件と直角三角形の合同条件と三角形の相似条件
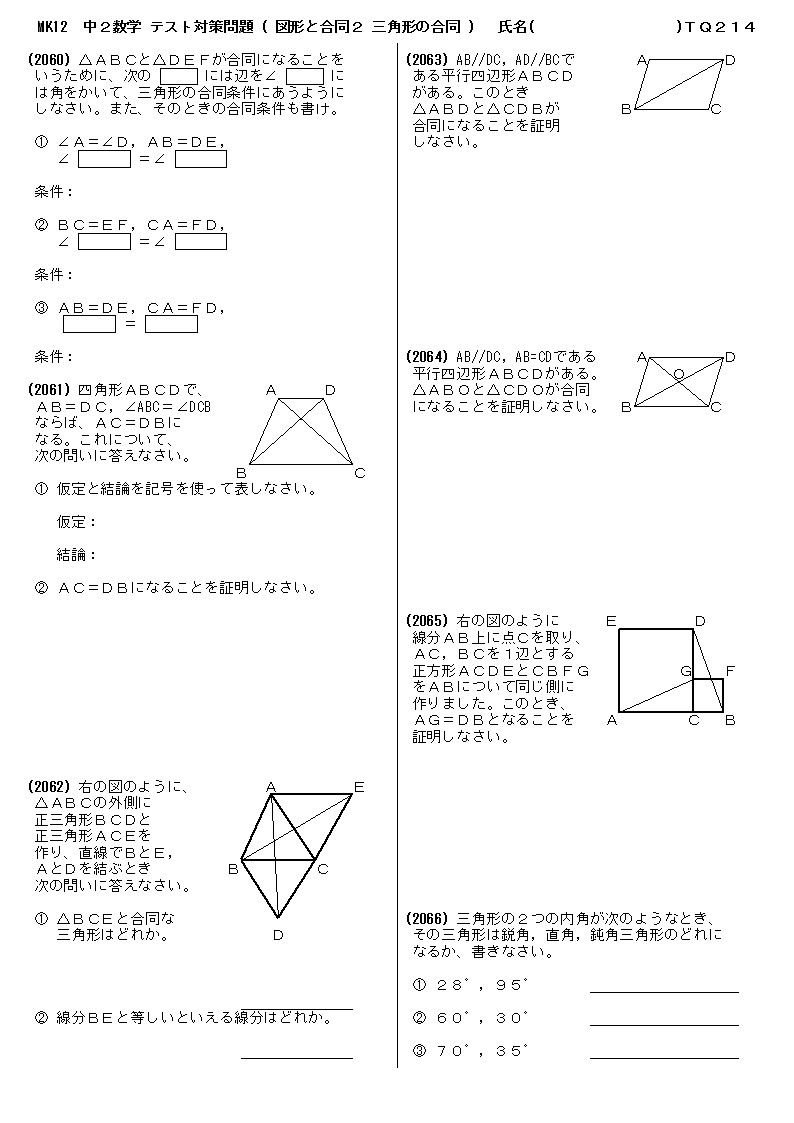


無料 中2数学 テスト対策 問題プリント 214 図形と合同2 三角形の合同



合同条件の選び方 家庭教師学参 群馬県のブログ



5分でわかる 三角形の3つの合同条件 Qikeru 学びを楽しくわかりやすく
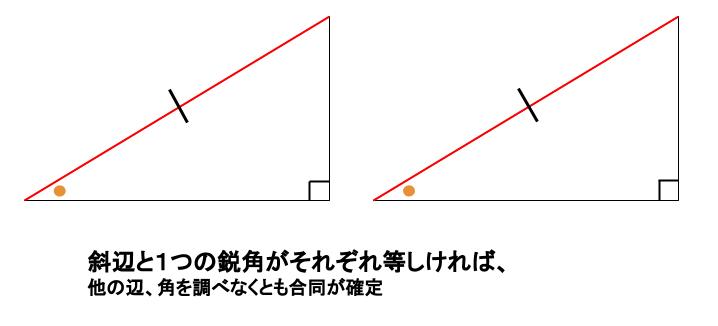


中学数学 直角三角形の合同条件 中学数学の無料オンライン学習サイトchu Su



三角形の合同条件



中2 数学 無料学習プリント教材



直角三角形の合同条件を使った証明とは なぜ2つ増えるのか 遊ぶ数学
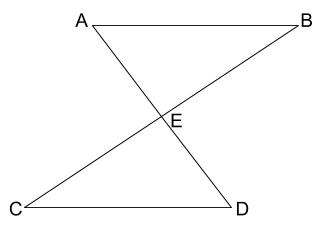


中学数学 三角形の合同条件 中学数学の無料オンライン学習サイトchu Su



直角三角形の合同条件とその証明 数学fun
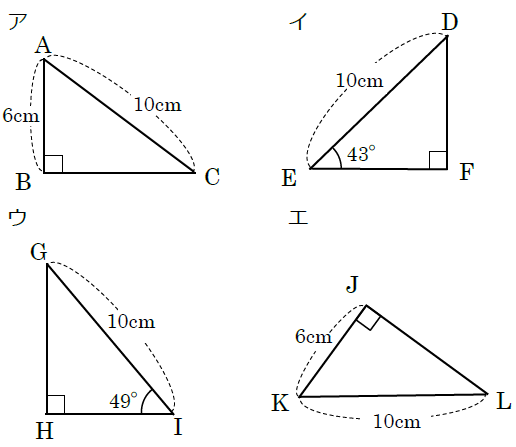


中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン



暗記必須 三角形の合同条件を見やすい図で一発理解しよう 高校生向け受験応援メディア 受験のミカタ



工程建设招标设标合同条件 第1部分 Word模板下载 招标 熊猫办公


三角形の合同条件 相似条件と合同条件の違いとは アタリマエ



中2数学 三角形の合同条件3 1辺とその両端角 例題編 映像授業のtry It トライイット


中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン



子供向けぬりえ 50 数学合同条件


合同条件 合同生效条件 合同终止条件 合同解除条件



三角形と四角形 三角形の合同の証明のしかた 中学数学 定期テスト対策サイト



スプリックス 直角三角形の合同条件 1 Youtube



2 の直角三角形の合同条件は何ですか 理由も付けて教えて頂けると助かります Clear



合同とは 三角形の合同条件 証明問題をわかりやすく解説 受験辞典



中2数学 チョー便利な直角三角形の2つの合同条件 Qikeru 学びを楽しくわかりやすく


三角形の合同条件 合同な図形の見つけ方 証明問題の基礎を身につけよう 数スタ



中2数学 三角形の合同の証明の解き方の手順 こいがくぼ翼学習塾


三角形の合同条件 まなびの学園



三角形の合同条件 Youtube
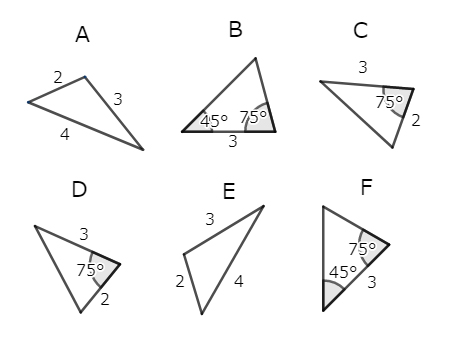


数学のアレ 何に役立つ 三角形の合同条件 同じ形の三角形を見つけて テストで5点くらいもらう 以外の使い方 1 2 ページ ねとらぼ
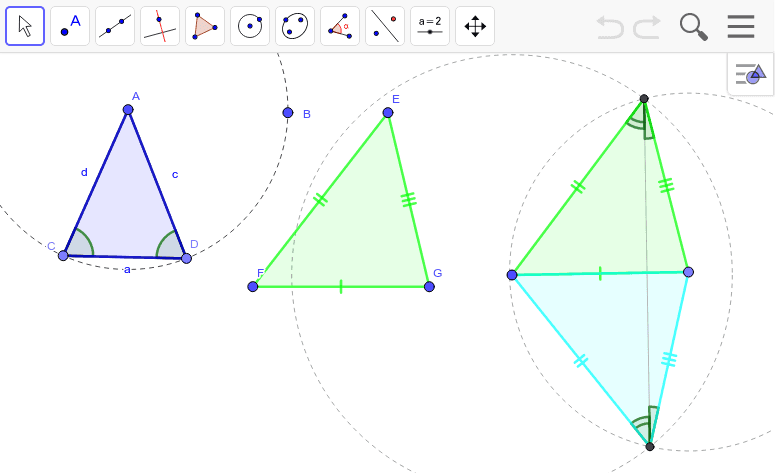


三角形の合同条件3辺 Geogebra
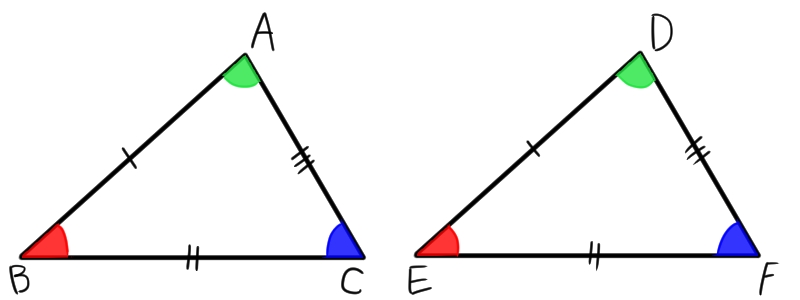


中学2年生の数学 証明 三角形の合同条件と証明の書き方 塾講師が数学をやりmath



中2数学 三角形の合同条件2 2辺とその間の角 例題編 映像授業のtry It トライイット



三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学



中2の証明問題を解く上で 必要な知識をまとめました プリントダウンロードできます 東大に文理両方で合格した男が綴る 受験の戦略


中学数学証明問題です 直角三角形の合同条件はわかるのですが Yahoo 知恵袋



合同な三角形をみつける On Vimeo



中学校数学 三角形と合同 三角形の合同条件 Youtube


平面図形の基礎


直角三角形の合同条件
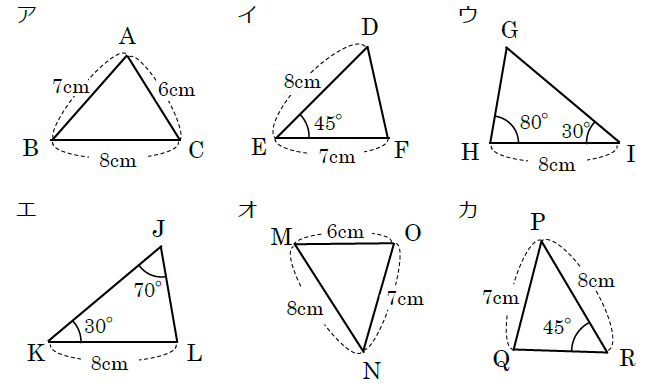


中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン



三角形の合同条件


合同な図形 小5 合同条件は超重要 算数の教え方教えますmother S Math Happy Study Support



三角形の合同条件 相似条件と合同条件の違いとは アタリマエ
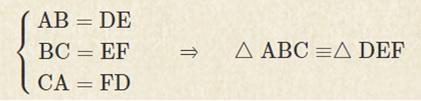


中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン
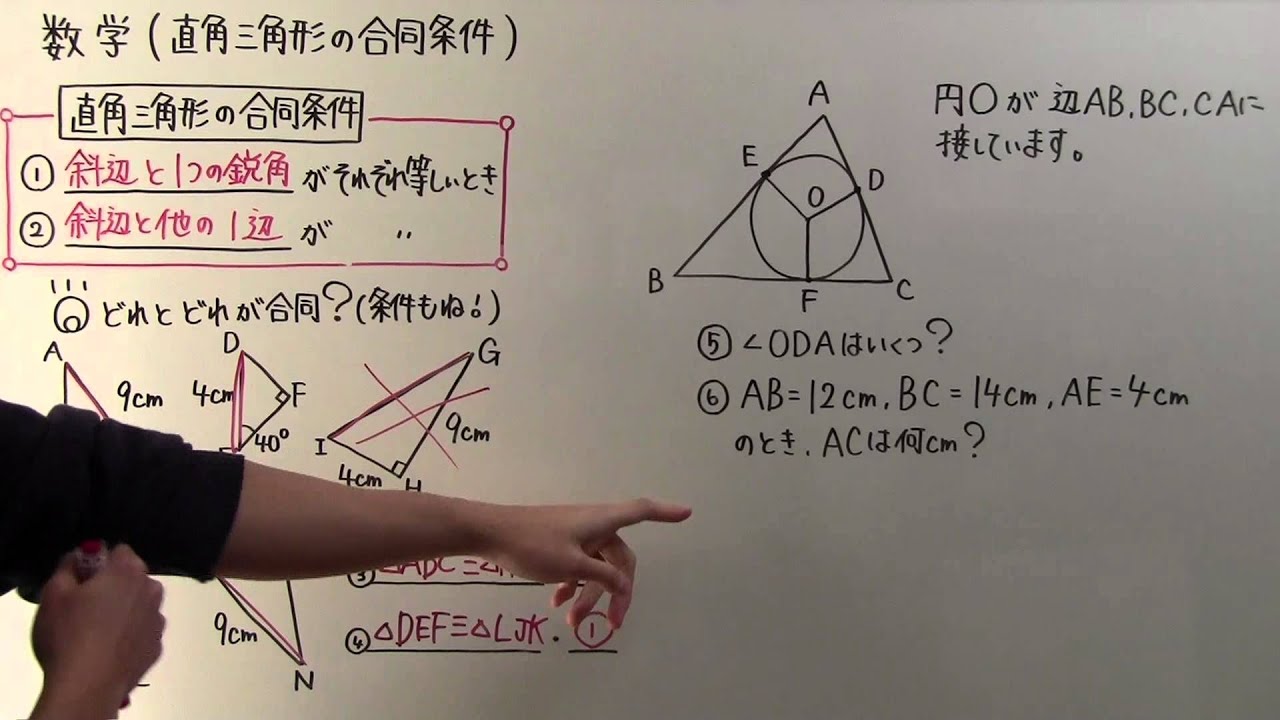


数学 中2 71 直角三角形の合同条件 Youtube


三角形の合同条件 思考力を鍛える数学


三角形の合同条件 板書


直角三角形の合同条件とそれを利用した証明 チーム エン


合同な図形とは 三角形の合同条件 教遊者
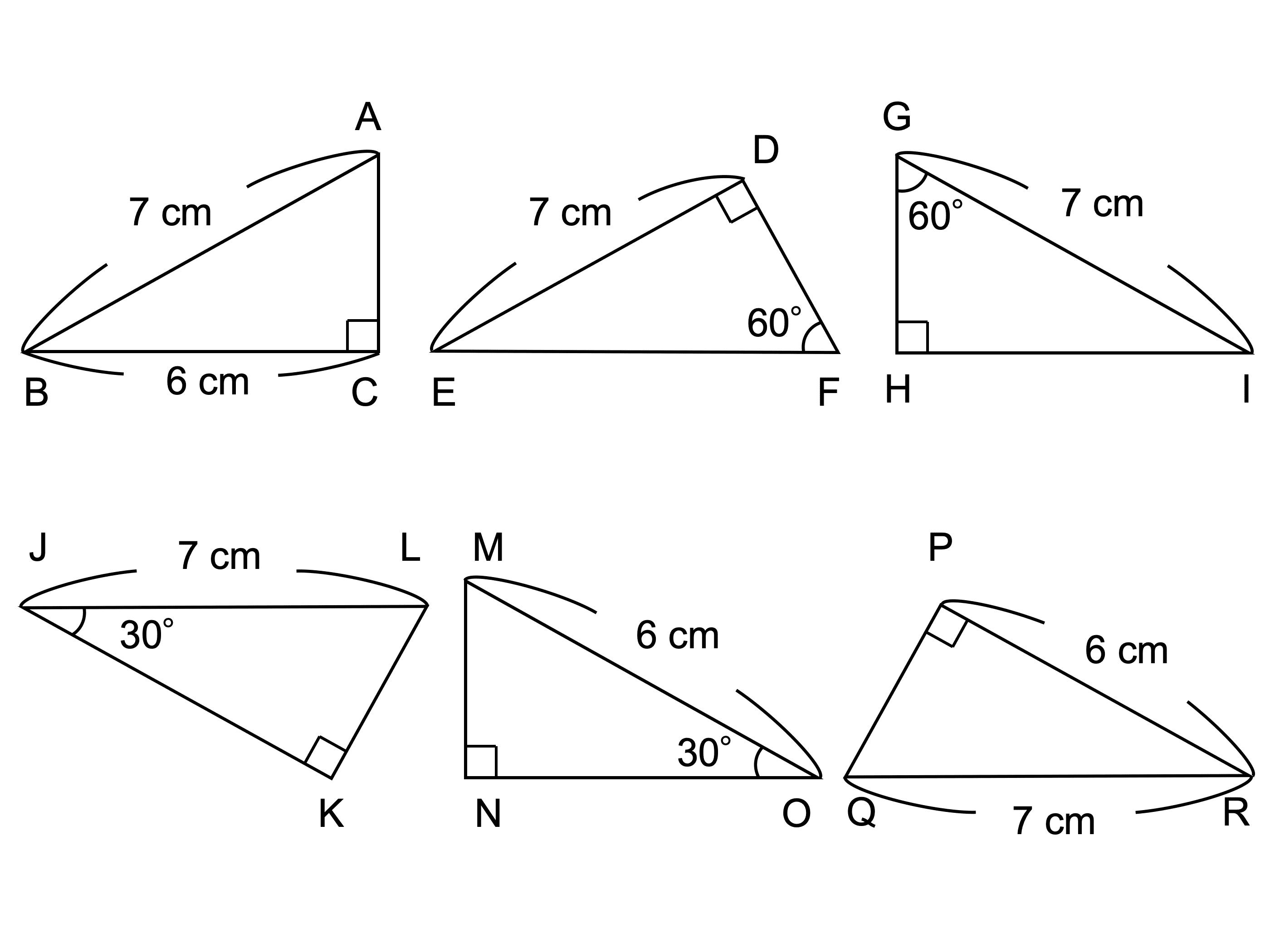


直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典
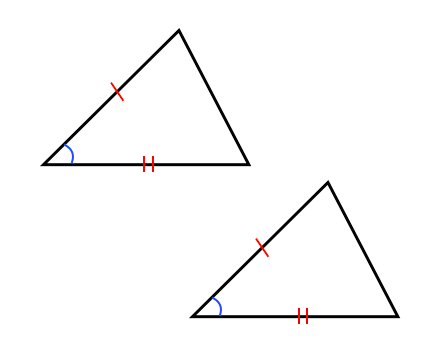


三角形の合同条件を知ろう 苦手な数学を簡単に


合同な三角形を見つける On Vimeo


合同な三角形をみつける On Vimeo



直角三角形の合同条件 証明のときに直角三角形が出てきたらこれ 中学や高校の数学の計算問題



保存版 三角形の合同条件と相似条件の6つのまとめ Qikeru 学びを楽しくわかりやすく



三角形の合同条件を使った証明問題 中学2年生の問題を解こう 身勝手な主張



中2数学 三角形の合同条件と証明 練習問題と詳しい解答
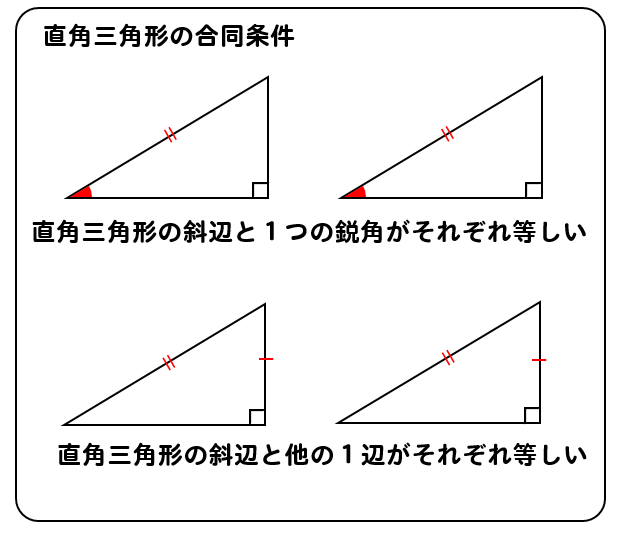


直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ


三角形の相似 合同条件 中学数学 理科 寺子屋塾の復習サイト



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン



三角形の合同条件と それに対応する面積公式 サブロウ丸


中学数学 三角形の合同条件 中学数学の無料オンライン学習サイトchu Su



三角形の合同ではなく直角三角形の合同条件で求めることはできま 中学数学に関する質問 勉強質問サイト


中学数学 図形の合同 図形の性質


三角形の合同の問題の解法 夢を叶える塾



中学数学より3 三角形の合同条件 身勝手な主張



三角形の合同条件と証明問題の解き方 数学fun
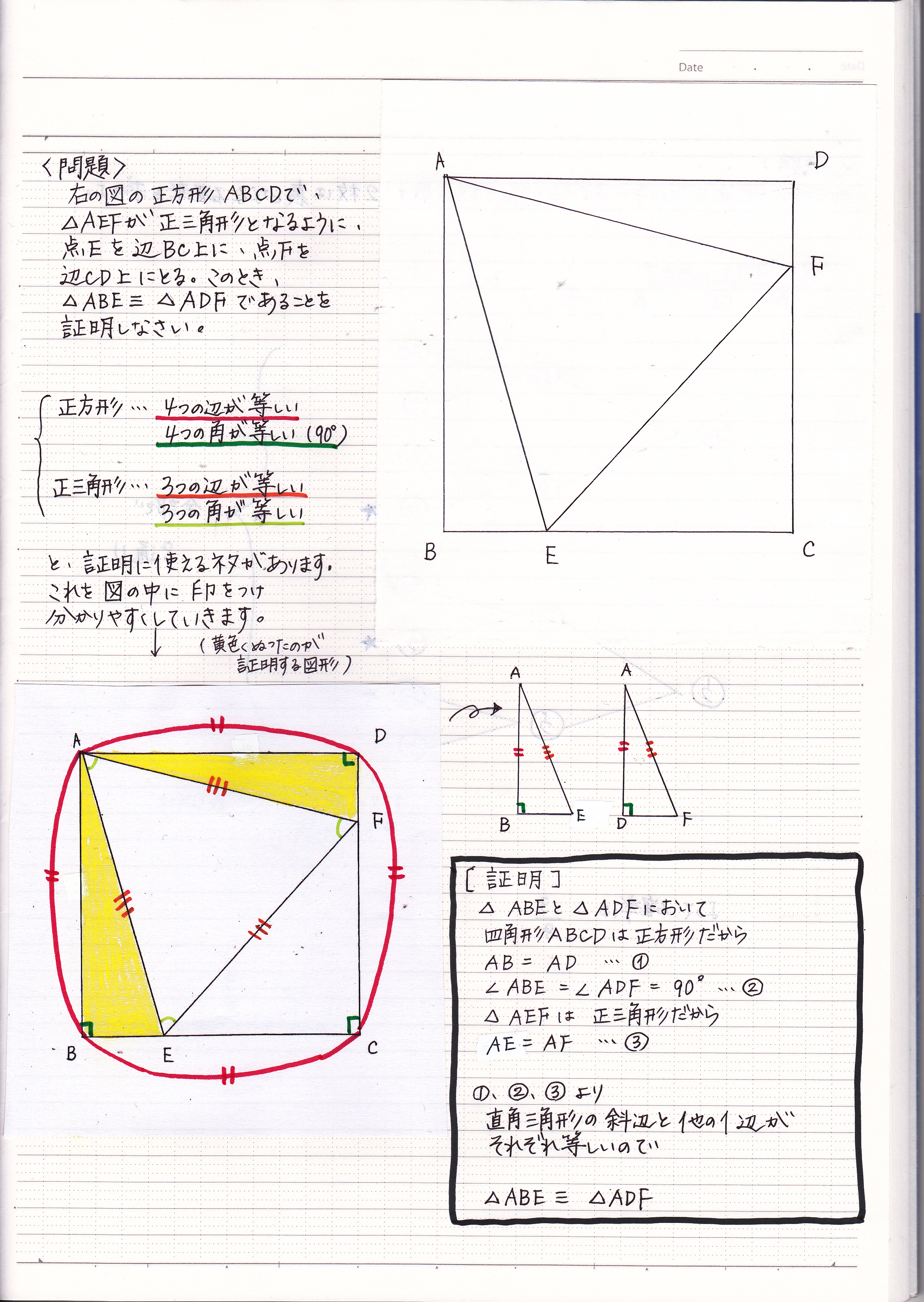


直角三角形の合同条件を使った証明問題の解き方 2 現役塾講師のわかりやすい中学数学の解き方



教えて下さい わからないです 1 Apc Bpdじゃないんですか Clear



三角形の合同条件 中学数学 By じょばんに マナペディア
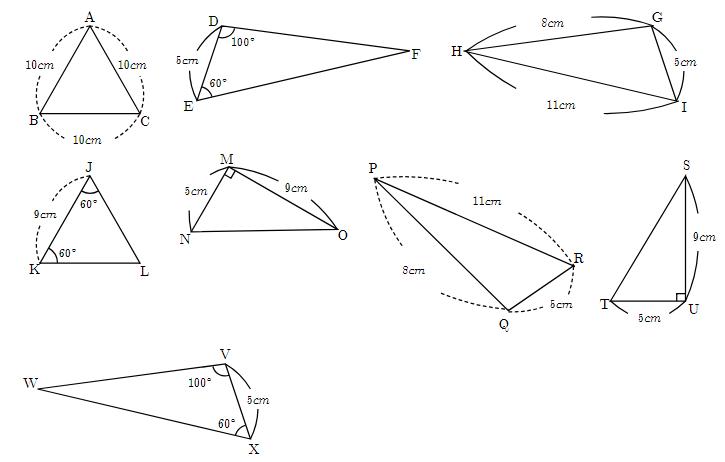


中2数学 三角形の証明の仕方 Pikuu
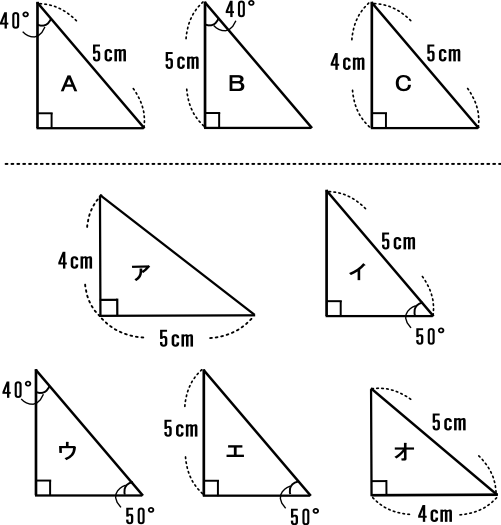


中学2年数学練習問題 直角三角形の合同条件と証明問題 図形と合同



三角形の合同条件 証明のときに絶対にしておかないといけない問題 中学や高校の数学の計算問題



直角三角形の合同条件再び 中学校2年生の数学 身勝手な主張
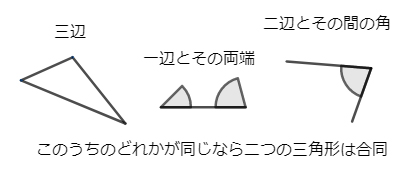


数学のアレ 何に役立つ 三角形の合同条件 同じ形の三角形を見つけて テストで5点くらいもらう 以外の使い方 1 2 ページ ねとらぼ


三角形の合同条件 Geogebra
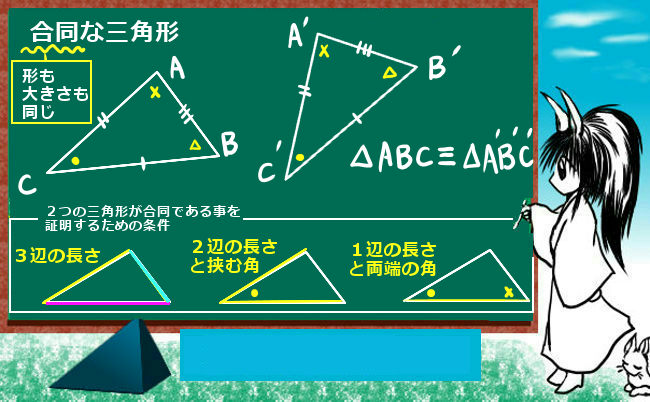


三角形の合同 理数系無料オンライン学習 Kori
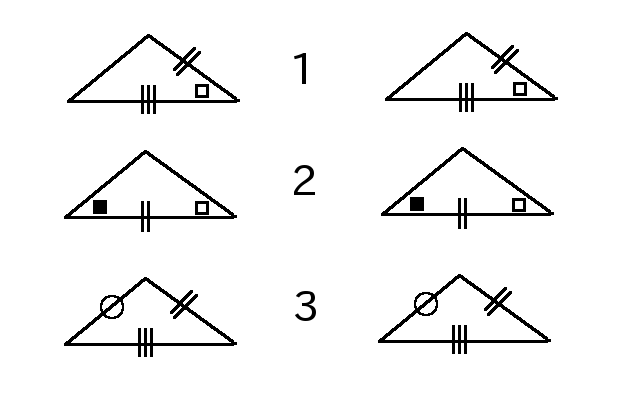


File 三角形の合同条件 Png Wikimedia Commons



三角形の合同条件



中2数学 三角形の合同条件2 2辺とその間の角 練習編 映像授業のtry It トライイット



合同と証明 Ict教材eboard イーボード


