半球の表面積の求め方はむずい?? こんにちは!この記事をかいてるKenだよ。そろそろ進撃したいね。 半球の表面積の公式 は簡単。 半径をrとすると、下にもあるので、面積は2r。 弧の長さは2。円周は2πrだから、πr倍すると、2πr 2 が半球の面積となる。 S:ぴったりですね。cosカーブの船形は面積を正確に表しているようですね。 S:実際にcosカーブで半球を作ってみました。は曲面S の面積を表す.ここで ∑ は分割されたすべての小矩形の和を意味する. 定理91 (曲面S の面積A) A= ∫∫ D jru rvjdudv (1) 例題91 半径Rの半球面の表面積Sは2ˇR2 である. (解)例91より r = (Rcos cosφ)i(Rcos sinφ)j (Rsin )k rφ= (Rsin sinφ)i(Rsin cosφ)j
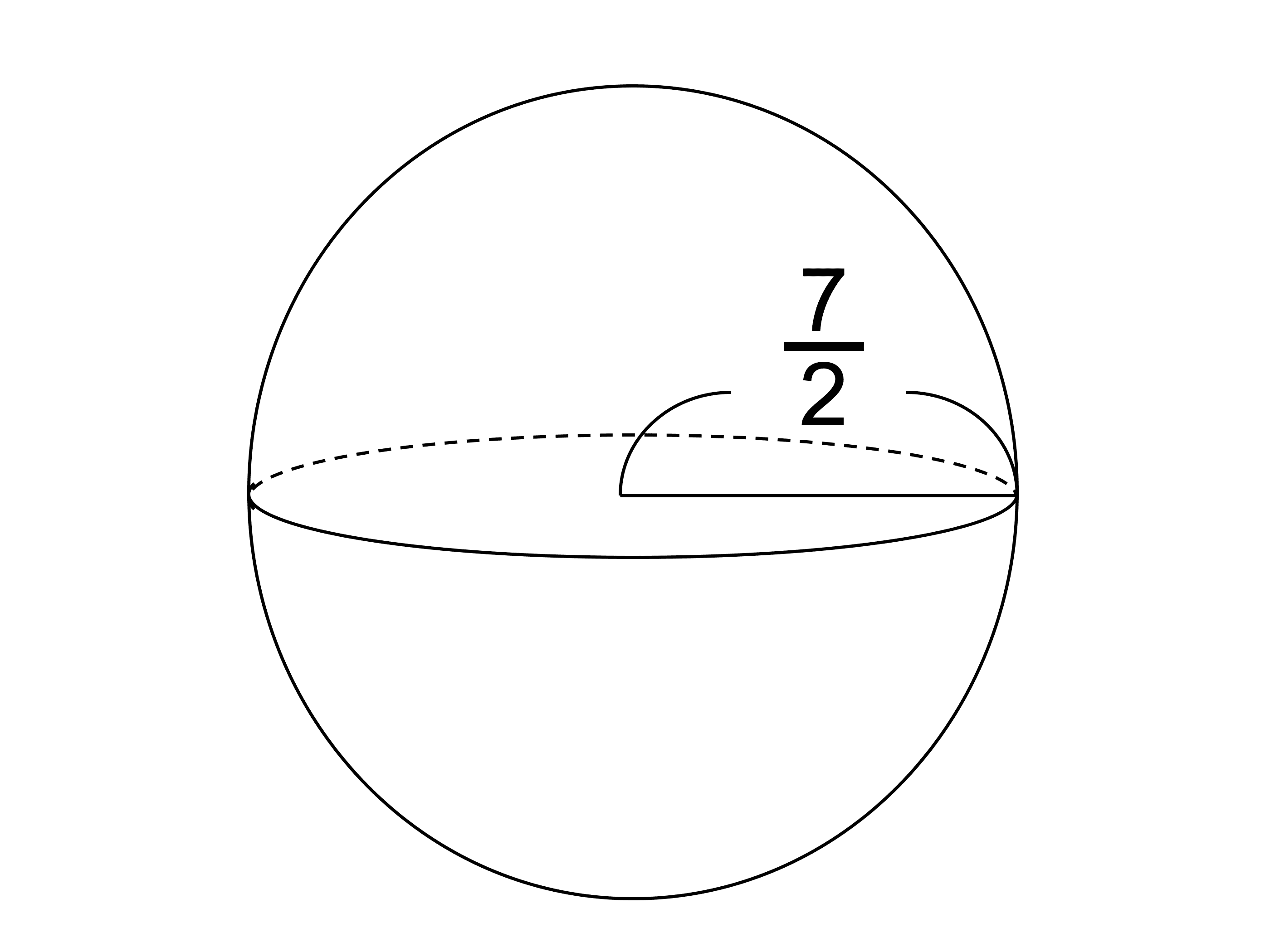
球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典
半球 の 表面積 計算
半球 の 表面積 計算-表面積 4πr^2×1/2+πr^2 体積 4/3πr^3×1/2 表面積は最後断面積も考慮しますよ(r=球の半径とする)球の表面積と体積 ここでは、球の表面積と体積を求める公式を紹介しましょう。 表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。 球の半
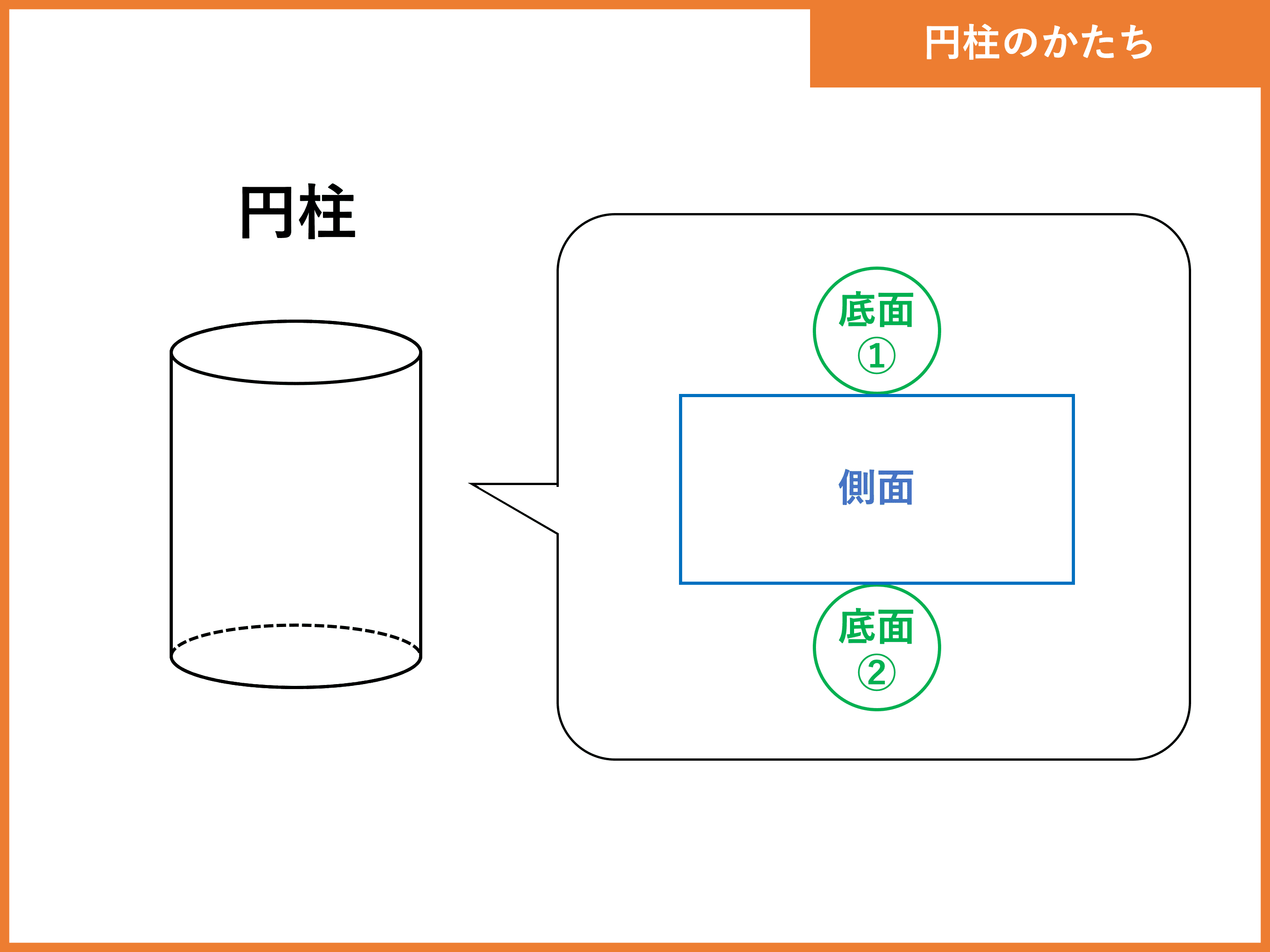


最も人気のある 円柱 表面積 公式 壁紙 配布
よって、半球の表面積は、 $2\pi R^2\pi R^2=3\pi R^2$ となります。 例題2:半径が $2\\mathrm{cm}$ の半球の表面積を計算してみましょう。 公式を使うと、いま示せばいいのは、「半球の表面積=円の面積×2」です。 さっきも書いたように、円周を底辺としたとき、「円は三角形、球の表面はsin形」と考えられるから、こんな図になる。 こうやって比較してみると、 円の面積 球の表面積球の表面積と体積 ここでは、球の表面積と体積を求める公式を紹介しましょう。 表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。 球の半
球の表面積 < (2) 2つの比較 (1)(2)より, < 球の表面積 < 方法②:輪切りにする 指針(考え方) この円柱の側面積= 球の表面積の公式と同じ式をしていることが分かる. あなたは今、球の表面積を求める公式を知らないものとします.球の表面積と体積 ここでは、球の表面積と体積を求める公式を紹介しましょう。 表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。 球の半いま示せばいいのは、「半球の表面積=円の面積×2」です。 さっきも書いたように、円周を底辺としたとき、「円は三角形、球の表面はsin形」と考えられるから、こんな図になる。 こうやって比較してみると、 円の面積 球の表面積
空間図形4回目は表面積の求め方です。いちおう円錐の側面積・表面積の公式も紹介しますが、この連載がめざすのは「応用・難問にであっても解けるような学力」です。よって、円とおうぎ形の基本まで立ち返って解説していきます。 Part 3 Part 3だから、(360/7)×球の表面積となってしまう。 s:半球の表面積は(1/2)×表面積なんてあたりまえだ。 s:でも、最初の三角形の面積の公式が求まるよ。 2πr×πr/2×α=2πr 2 だから、α=2/π 最初の三角形の面積=2/π×底辺×高さ球の表面積の求め方の公式はおぼえにくい?? こんにちは!この記事をかいているKenだよ。豚肉を今日もいためたね。 球の表面積の求め方には公式があるんだ。 球の半径をrとすると、その表面積は、 4πr^2 になるよ。 つまり、 4 × 円周率 × 半径 × 半径



球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



9月29日更新 高校入試を見る 青森県公立高校入試 数学 1 成績 上がってます 根城学習塾 八戸市
だから、(360/7)×球の表面積となってしまう。 s:半球の表面積は(1/2)×表面積なんてあたりまえだ。 s:でも、最初の三角形の面積の公式が求まるよ。 2πr×πr/2×α=2πr 2 だから、α=2/π 最初の三角形の面積=2/π×底辺×高さ表面積は3通りの方法を解説します。 積分の感覚をつかむよい練習になります。 球の体積と表面積の公式について まずは証明の前に,球の表面積と体積に関して認識しておくべきことを整理しておきました。 以下の語呂合わせで覚える方法が有名です:球の表面積と体積1 名前 次の式を書きなさい。 21 ①半径 の球の体積 を求める式。 3# ②半径 の球の表面積 を求める式。 3# 次の球の表面積と体積を求めなさい。 cm 表面積: 体積: cm 表面積: 体積: 右の図は、半径が cmの球を、中心を通る平面で切って



簡単公式 半球の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく


球の表面積 体積 チーム エン
数学 半球の体積、表面積 半径4の半球があります。その半球の体積、表面積を教えてください! 質問No《半球の表面積の求め方》 半球の表面積 =球の表面積の半分+半球の切り口である直径4cm(半径2cm)の円の面積であることから 答え cm² ~立体の体積・表面積を求める公式まとめ~ 立方体・直方体の体積の求め方球の表面積の公式、S=4πr 2 とは違ってしまう。 これは、円周の長さを x 方向に積分するときに、xを微小増加させたときの表面積の変化量が x=0 付近と x=r 付近で異なり、x=r 付近の方が表面積の増加量が大きいためと考えられる。



球の体積 表面積 中1数学 空間図形9 Youtube



印刷可能 円錐 の 表面積 問題 無料の印刷可能なイラスト素材
半径がaの球を書きます。中心は原点にとって下さい。そこから積分を使って球の表面積を出して下さい。途中過程を宜しくお願いします。 一般に、回転体の表面積を求める問題と考えましょう。滑らかな関数f(x)によるy=f(x) ≧ 0 (x∈a,b)の表面積 4πr^2×1/2+πr^2 体積 4/3πr^3×1/2 表面積は最後断面積も考慮しますよ(r=球の半径とする)もし球の表面積の公式を忘れてしまったとしても、円柱の側面積と同じになることを知っていれば、公式を導き出すことができます。 練習問題:球の体積と表面積 q1 次の半球の体積と表面積を計算しましょう。なお、円周率は$π$とします。
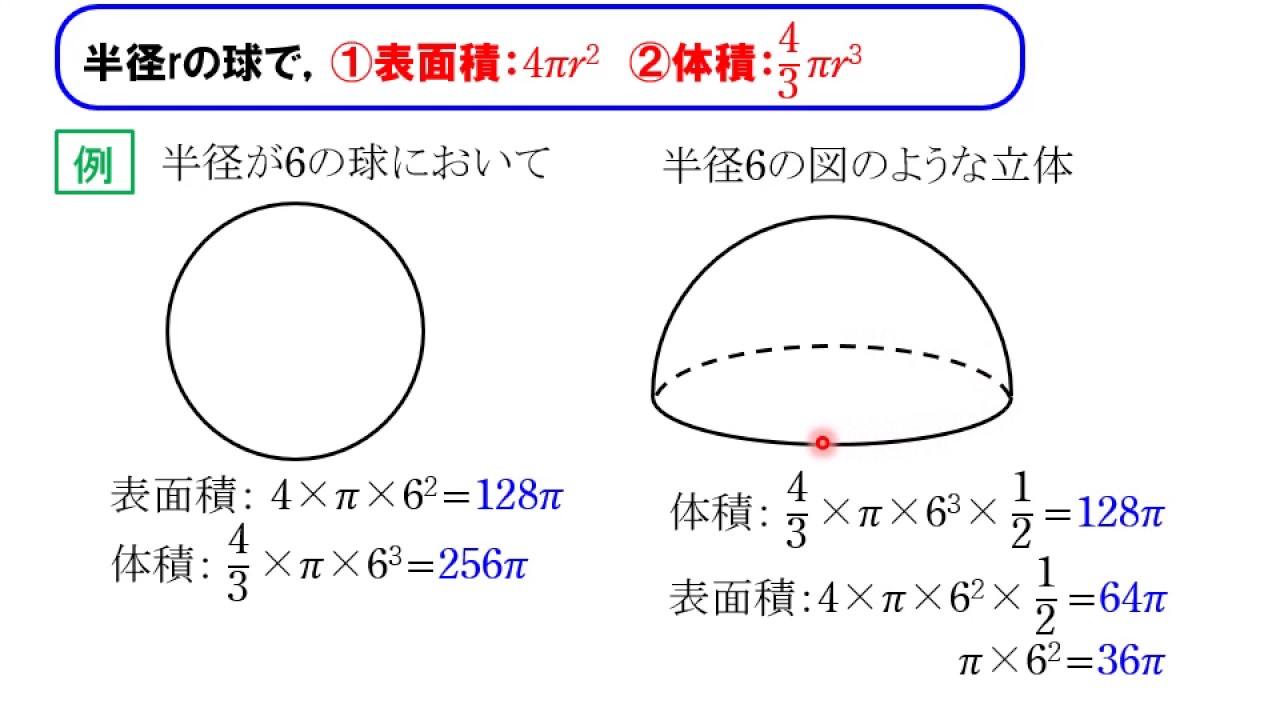


空間図形18 球の表面積と体積 Youtube
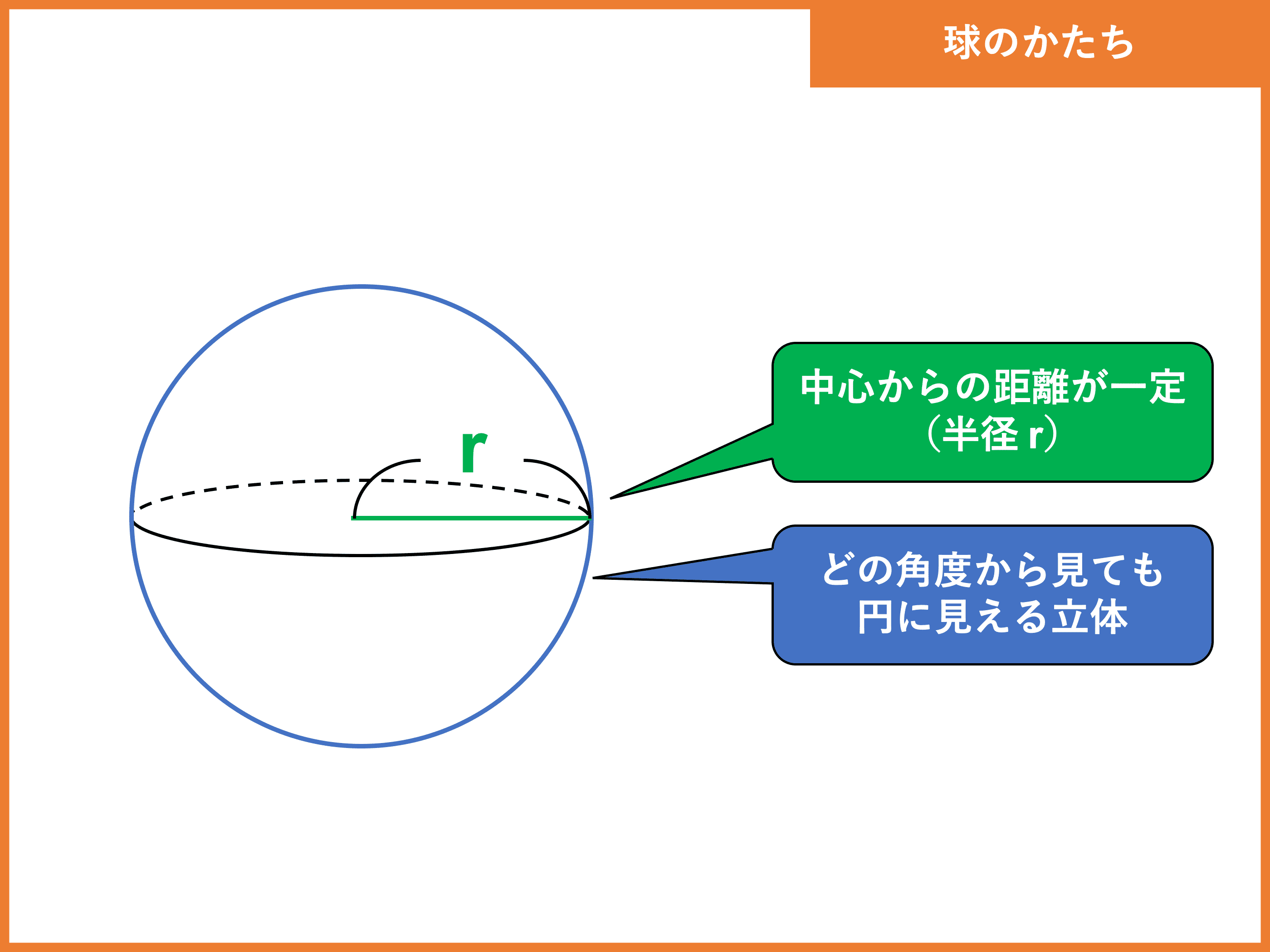


球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典
では実際に体積と表面積(曲面積)を求める問題を1問ずつ練習してみましょう。 練習1 円柱 の にある部分の体積 と表面積 を求めなさい。 練習2 球 の にある部分の体積 と表面積 を求めなさい。 4.練習問題の答え 解答1 概形と底面は下の図のようになる。では実際に体積と表面積(曲面積)を求める問題を1問ずつ練習してみましょう。 練習1 円柱 の にある部分の体積 と表面積 を求めなさい。 練習2 球 の にある部分の体積 と表面積 を求めなさい。 4.練習問題の答え 解答1 概形と底面は下の図のようになる。いま示せばいいのは、「半球の表面積=円の面積×2」です。 さっきも書いたように、円周を底辺としたとき、「円は三角形、球の表面はsin形」と考えられるから、こんな図になる。 こうやって比較してみると、 円の面積 球の表面積


ポテト一郎



Twitter पर さくら塾 四日市 うちの息子が 俺 球の表面積と体積の公式が覚えられんから アルキメデスの発見を使って毎回導いてるんよ と言ってて はぁ と思ったがこれのことか ウケる
前の記事「半球の高さを n 等分すると表面積はどうなるか?」の答えを出すために、その前に「球の表面積」をどうやって求めるかを考えた。 1つ目は「球の体積 Vもし球の表面積の公式を忘れてしまったとしても、円柱の側面積と同じになることを知っていれば、公式を導き出すことができます。 練習問題:球の体積と表面積 q1 次の半球の体積と表面積を計算しましょう。なお、円周率は$π$とします。半径がaの球を書きます。中心は原点にとって下さい。そこから積分を使って球の表面積を出して下さい。途中過程を宜しくお願いします。 一般に、回転体の表面積を求める問題と考えましょう。滑らかな関数f(x)によるy=f(x) ≧ 0 (x∈a,b)の



球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ



優雅 球体 表面積 求め 方 壁紙 配布
表面積 4πr^2×1/2+πr^2 体積 4/3πr^3×1/2 表面積は最後断面積も考慮しますよ(r=球の半径とする)



球の表面積 Sgk Note



回転体の表面積 側面積 身勝手な主張



07 図形の計量 P 224 226 立体の見方と調べ方 球の表面積と体積 Youtube


Www1 Iwate School Jp Action Common Download Main Upload Id 1248



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典


Http Www Kiyose Ed Jp Res Projects Project Education Page 002 001 304 2suugaku Horita04 Pdf



中1数学 空間図形 定期テスト編 Nazal S Blog


優雅 球体 表面積 求め 方 壁紙 配布



球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく



10 号 球の表面積の公式学習用数学教材 Astamuse



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ


2



お時間ある方教えてください Clear



球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



面白数学 球の表面積 円の面積 4の理由 東大生の高校数学ブログ



最も人気のある 円柱 表面積 公式 壁紙 配布



球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



愛されし者 側 面積 求め 方 壁紙 配布



この半球の表面積の求め方の式が分かりません 答えは48pcm になるらしいです Clear


優雅 球体 表面積 求め 方 壁紙 配布



数学 中学2 図形 中学数学に関する質問 勉強質問サイト



中学数学 円の面積の求め方 の公式を1発で覚えてしまう裏技 Qikeru 学びを楽しくわかりやすく



中1数学 球の計算のポイント 中学生 数学のノート Clear



中1 数学 6 5 球の体積 表面積 Youtube


Http Www Qingdaojs Org Old Rinjikyuukoutyuunoosirase Kadai Kadai7 Suugaku7 Pdf



新しい 球体 体積 求め 方 壁紙 配布



積分 試行錯誤



3次元極座標をやる前に 復習をします 1 三角関数の復習 高校数学 前期 2 2次元極座標の復習 高校の数学b Ppt Download


Www Edu City Narita Chiba Jp Jhs Nakadai News Files Kuukanzukeikaitou Pdf



球の表面積を重積分を使って計算してみた Youtube



数学公式集 円錐の表面積 球と半球の表面積と体積 高校入試 Youtube



10 号 球の表面積の公式学習用数学教材 Astamuse


Qsj1984 Com Wp Content Uploads 07 5ab4edf75cbb772b2818b0c Pdf



立体 の 表面積 子供のためのちょうど着色ページ



球の体積の公式を積分を使わず導く 中受でも出るかも 兄中学生活



簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



球と立体角 Yoshihiraのスペース


Www Juen Ac Jp Math Nakagawa Arithmeticp Pdf



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典



球の体積 表面積 中学生にも納得のいく方法で 積分でも出します Youtube


簡単公式 半球の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



中学数学 円の面積の求め方 の公式を1発で覚えてしまう裏技 Qikeru 学びを楽しくわかりやすく



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



優雅 球体 表面積 求め 方 壁紙 配布



簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく



球欠と球冠 Fukusukeの数学めも



10 号 球の表面積の公式学習用数学教材 Astamuse



オンライン自習室 00 21 00 Youtube
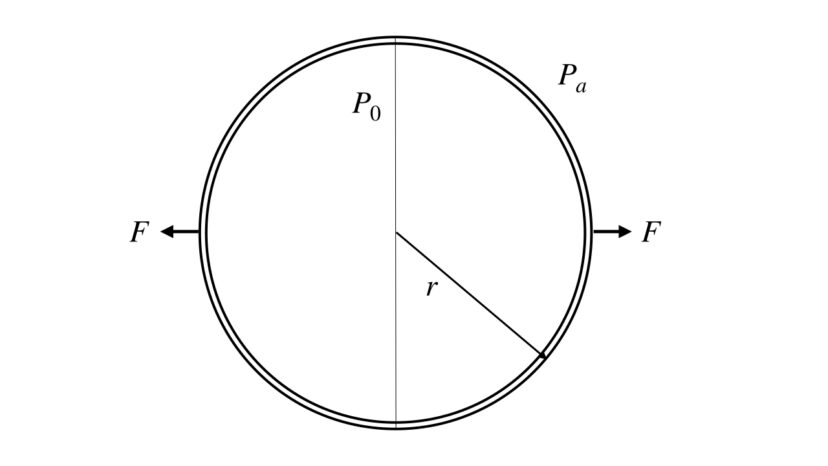


球殻を引き離す力の計算



簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく



新しい 球体 体積 求め 方 壁紙 配布


Http Www Kurims Kyoto U Ac Jp Kyodo Kokyuroku Contents Pdf 1392 8 Pdf



10 号 球の表面積の公式学習用数学教材 Astamuse



球の表面積と円の面積 Okwave



面白数学 球の表面積 円の面積 4の理由 東大生の高校数学ブログ



教えてください Clear
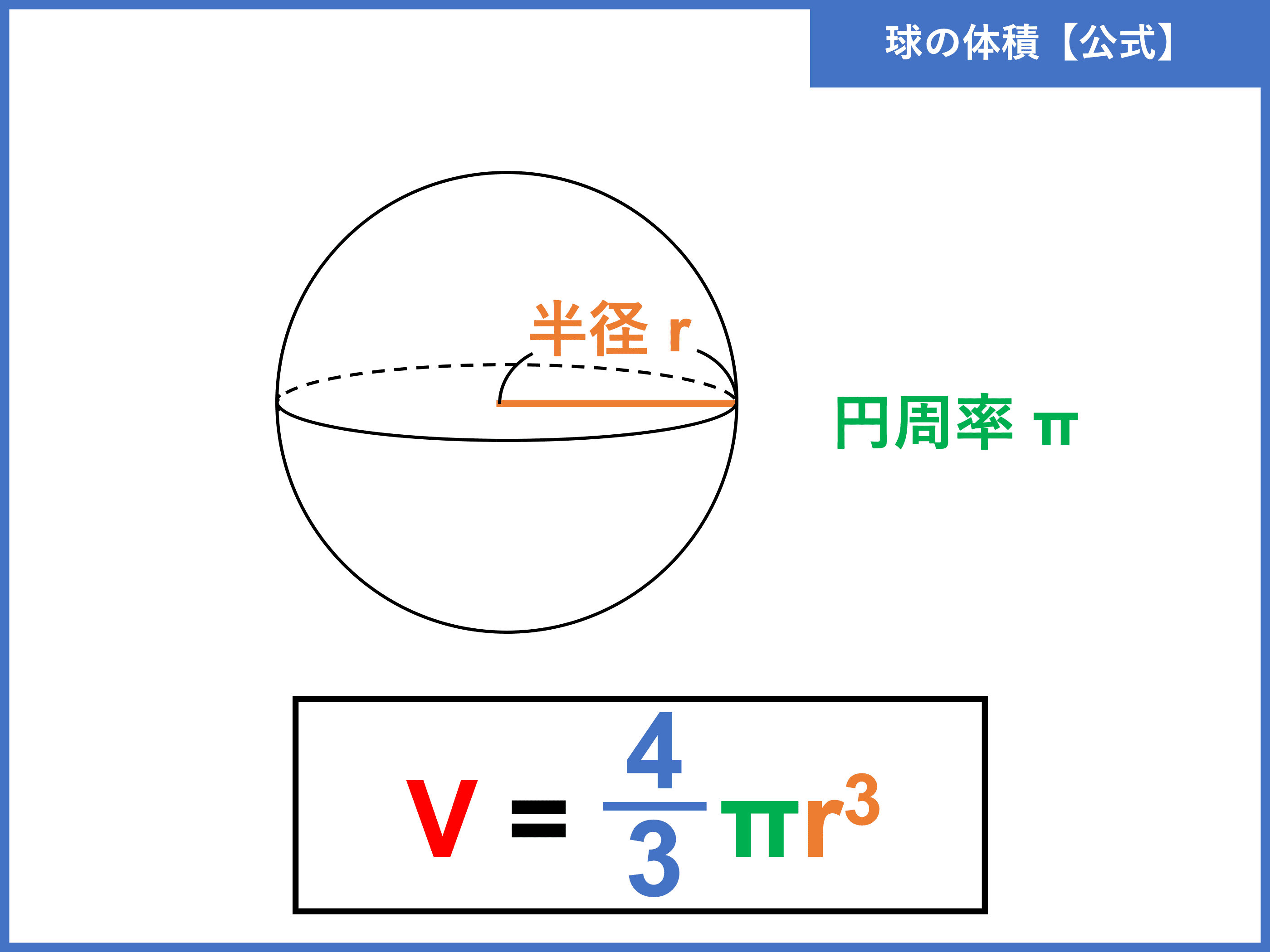


球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典


Www City Hadano Kanagawa Jp Www Contents Simple Kuukan460 Pdf



表面積の部分で 公式は4pr2乗なのに 4pr2乗に半円なので 2 2分の1 Clear



中1数学 球 練習編 映像授業のtry It トライイット



何故その解き方になるのかわからないので教えて下さい おねがいします Clear



簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく


2


2


2



球と立体角 Yoshihiraのスペース



この表面積の問題教えて欲しいです 全然分からなくて Clear



球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ
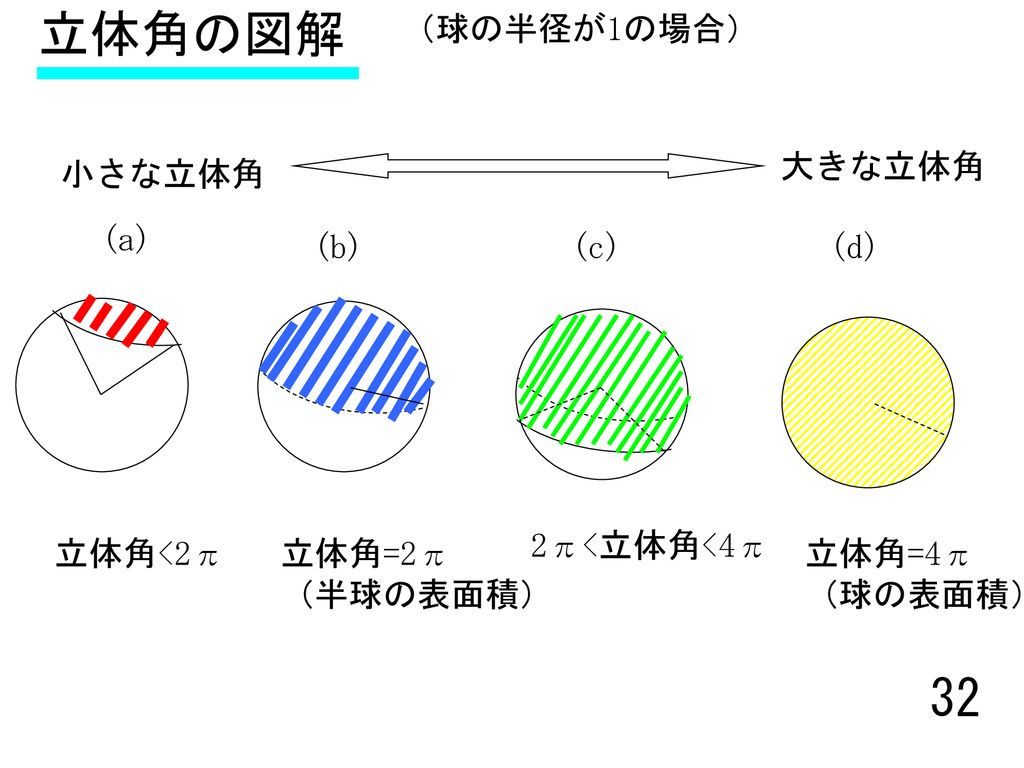


3次元極座標をやる前に 復習をします 1 三角関数の復習 高校数学 前期 2 2次元極座標の復習 高校の数学b Ppt Download



兵庫県の問題を教えてくださいm M Clear



球冠 Wikipedia


Www Saga Ed Jp Kenkyu Kenkyu Chousa R1 Documents 6 Chusu Kontentu B 1 6sho2 Kufurei Pdf


Http Shinobazudou Web Fc2 Com Konin Math Txt Txt Konin Math 27 Pdf



中学2年 図形 中学数学に関する質問 勉強質問サイト



中1数学 球の計算のポイント 中学生 数学のノート Clear
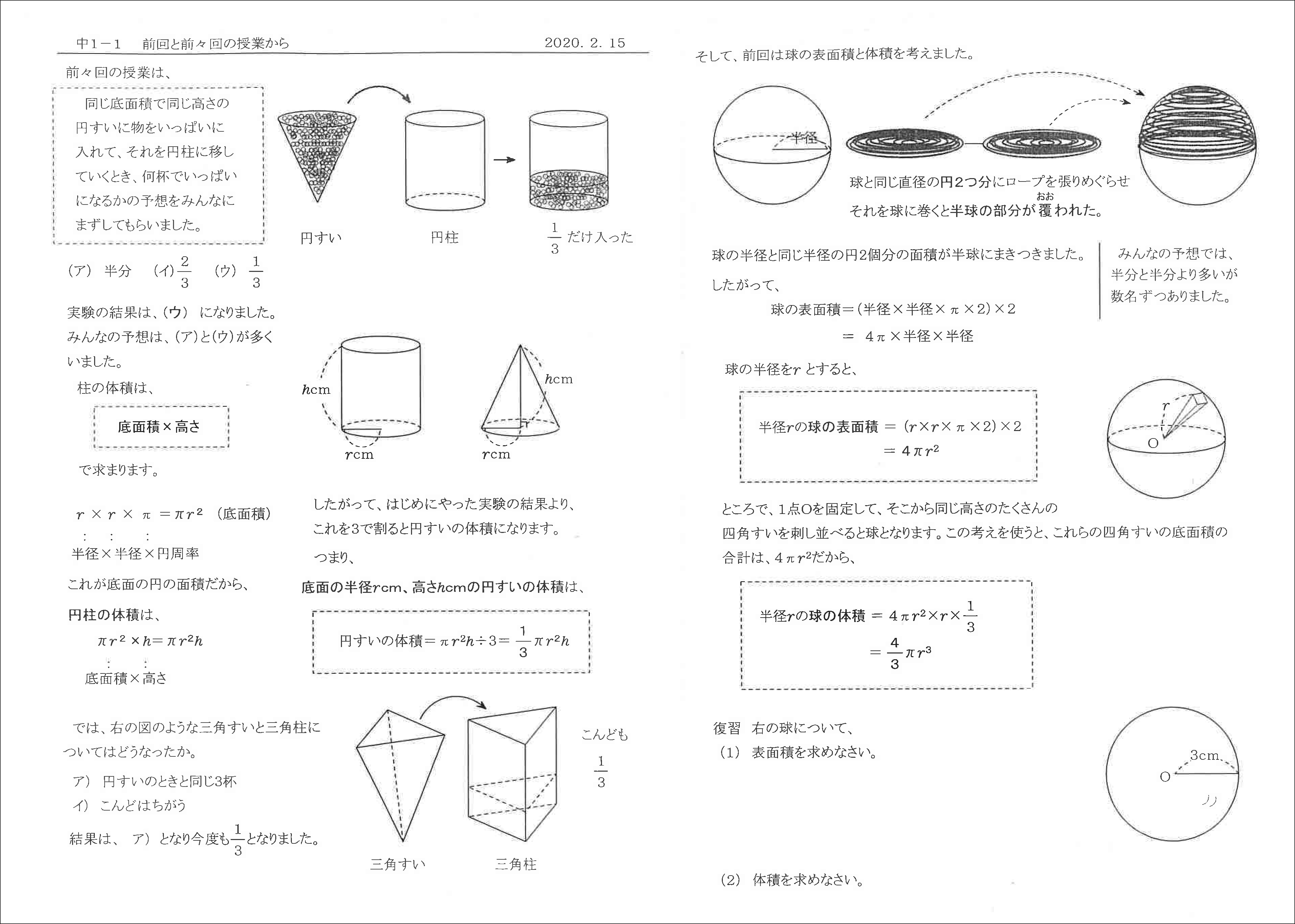


中1 立体の体積 東京女子学園中学校 高等学校



球の体積と表面積 Youtube


Http Www City Nanao Ishikawa Jp Notokashimatyu Kyouka gakusyuu Kukanzukeimondai Pdf



簡単公式 半球の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



中1数学 P377問題7 Youtube



中1数学 球の表面積と体積の求め方と練習問題 やすひこ先生の中学生授業log



球と立体角 Yoshihiraのスペース



高校受験数学 球の体積と表面積の授業映像 プリント無料配布 Youtube スタディカフェ


Www Toin H Wakayama C Ed Jp Toinjhs Files Pdf



โน ตของ 中1数学 球の体積と表面積 ช น Junior Clear



中1 数学 空間図形12 立体の表面積 18分 Youtube


Http Www Pref Osaka Lg Jp Attach 6629 Jmw 1b6 7 Pdf


