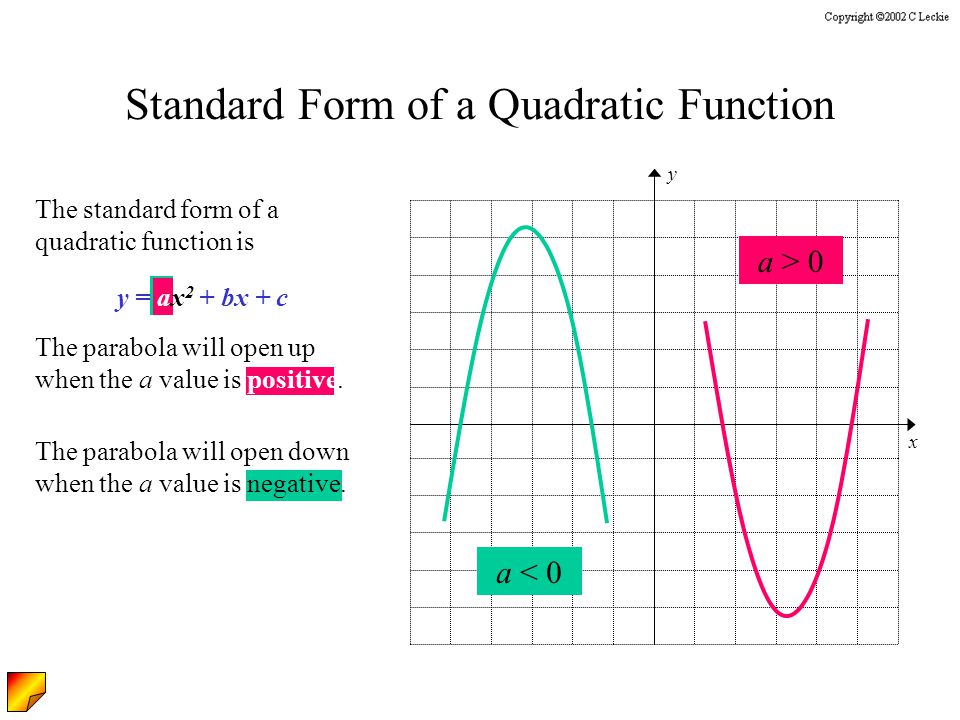
Do you think the rate of change will be the same at every point on the parabola?Thus, the equation of the parabola with axis parallel to the xaxis is of the form x=Ay 2 By C and the equation of the parabola with axis parallel to the yaxis is of the form y=Ax 2 Bx C 4 Parametric Equations of the Parabola y 2 = 4ax The parametric equations of the parabola y 2 = 4ax are x = at 2, y = 2atThe graph of the equation y =ax^2 bx c, where a, b, and c are constants, is a parabola with axis of symmetry x = 3 Find b/a Geometrically speaking, a parabola is defined as the set of points that are the same distance from a given point and a given line
Graphing Quadratic Functions Y Ax 2 Bx C Graphing Quadratic Functions Today We Will Understand How The Coefficients Of A Quadratic Function Influence Ppt Download
Persamaan parabola y = ax^2 + bx + c
Persamaan parabola y = ax^2 + bx + c-The parabola y=x^2 is just one of the many parabolas with vertical axis and vertex at the origin In fact, these parabolas are the graphs of equations of the form (2) y=ax^2 where a is a nonzero real number If a is positive, then the parabola opens upward while if a is negative it opens down To sketch the FIGURE 8Find the parabola of the form y=ax^2b which best fits the points (1,0), (2,2), (3,4) by minimizing the sum, S, of squares of the vertical distances from the above points to the parabola given by


Content Transformations Of The Parabola
0 $$ it opens downwards The axis of symmetry The axis of symmetry is the line $$ x = \frac{b}{2a} $$Given verbal, graphical, or symbolic descriptions of the graph of y = ax^2 c, the student will investigate, describe, and predict the effects on the graph when a is changedBest Answer Suppose that we have an equation y=ax^2bxc whose graph is a parabola with vertex (3,2), vertical axis of symmetry, and contains the point (1,0)
User Find the line of symmetry for the parabolaFind the equation of the following parabola of the form y = ax 2 The graph is of the form y = ax 2 The given coordinate is ( 2, 1 ) So x = 2 and y = 1 are on the curve Substitute and solve Parabolas of the form y = a(xb) 2 Example Complete the table of values for the equation y= (x2) 2 Plotting these points and joining with aWeegy The value of a is 2, The line of symmetry of the parabola whose equation is y = ax^2 4x 3 is x = 2 Princess MelPoints 300 User What is the xcoordinate of the vertex of the parabola whose equation is y = 3x^2 9x?
Free Parabola calculator Calculate parabola foci, vertices, axis and directrix stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie PolicySince a parabola \(\normalsize{y=ax^2bxc}\) is specified by three numbers, it is reasonable to suppose that we could fit a parabola to three points in the plane This is indeed the case, and it is a useful idea In this step we see how to algebraically fit a parabola to three points in the Cartesian plane This involves recalling, or learningFind the equation of the following parabola of the form y = ax 2 The graph is of the form y = ax 2 The given coordinate is ( 2, 1 ) So x = 2 and y = 1 are on the curve Substitute and solve Parabolas of the form y = a(xb) 2 Example Complete the table of values for the equation y= (x2) 2 Plotting these points and joining with a



View Question A Parabola With Equation Y Ax 2 Bx C Has A Vertical Line Of Symmetry At X 1 And Goes Through The Two Points 1 3 And 2 2 The Quadratic



This Is What The Problem Says Assuming All Parabolas Are Of The Form Y Ax 2 Bx C Drag And Drop The Brainly Com
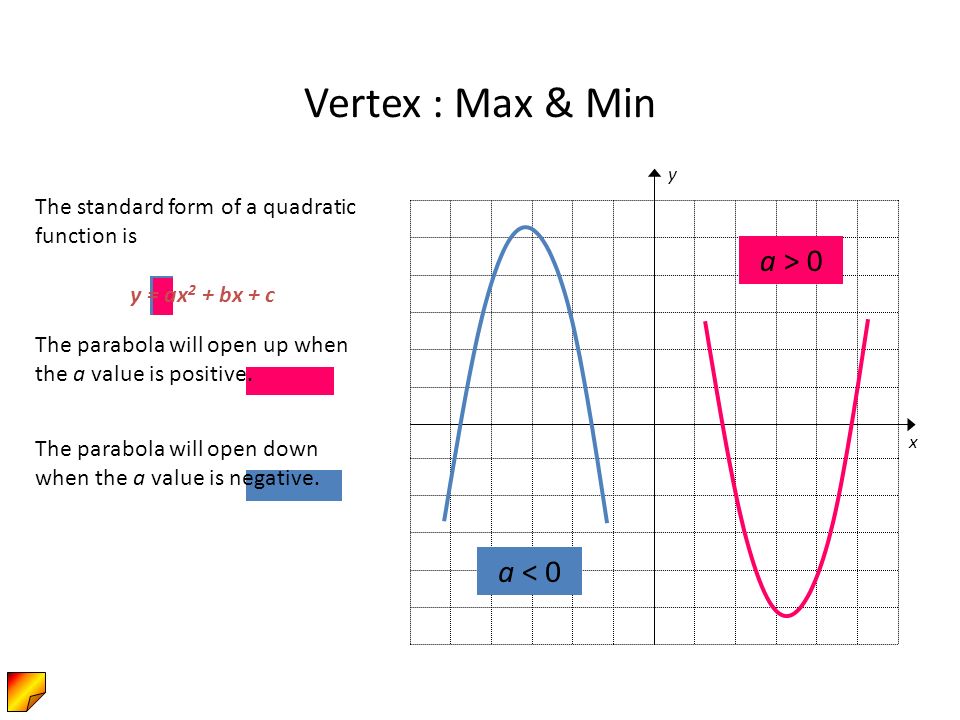
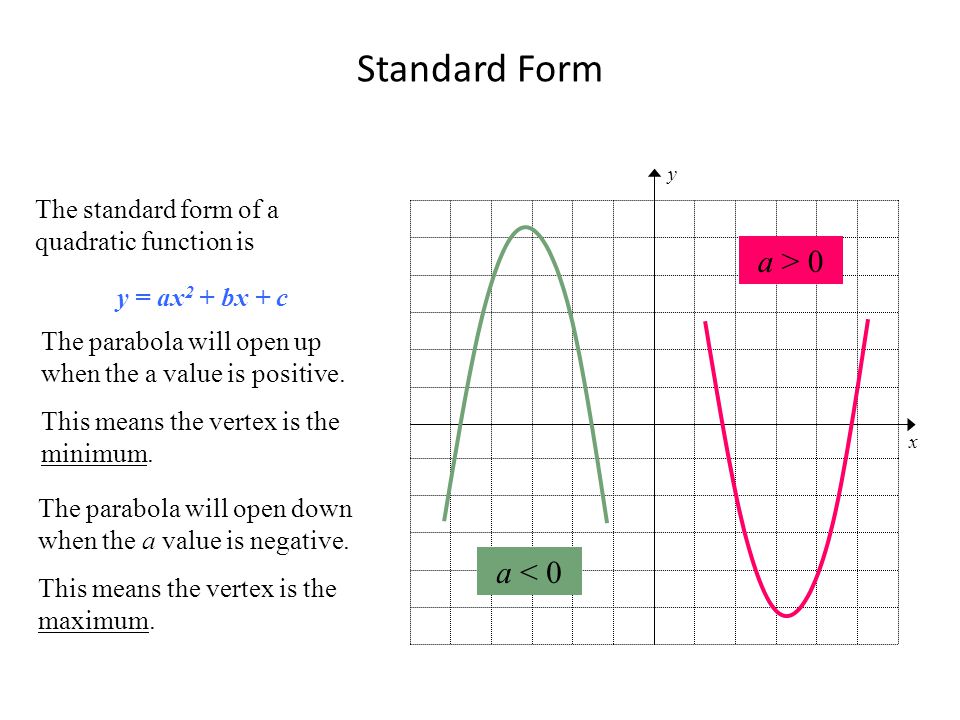
The standard form of a parabola's equation is generally expressed $ y = ax^2 bx c $ The role of 'a' If $$ a > 0 $$, the parabola opens upwards ;A parabola is the arc a ball makes when you throw it, or the crosssection of a satellite dish As long as you know the coordinates for the vertex of the parabola and at least one other point along the line, finding the equation of a parabola is as simple as doing a little basic algebraConic Sections Parabola We know that a parabola has a basic equation y = ax 2 The vertex is at (0, 0) The distance from the vertex to the focus and directrix is the same Let's call it p Focus Directrix p p y = ax 2 9 Conic Sections Parabola Find the point for the focus and the equation of the directrix if the vertex is at (0, 0)
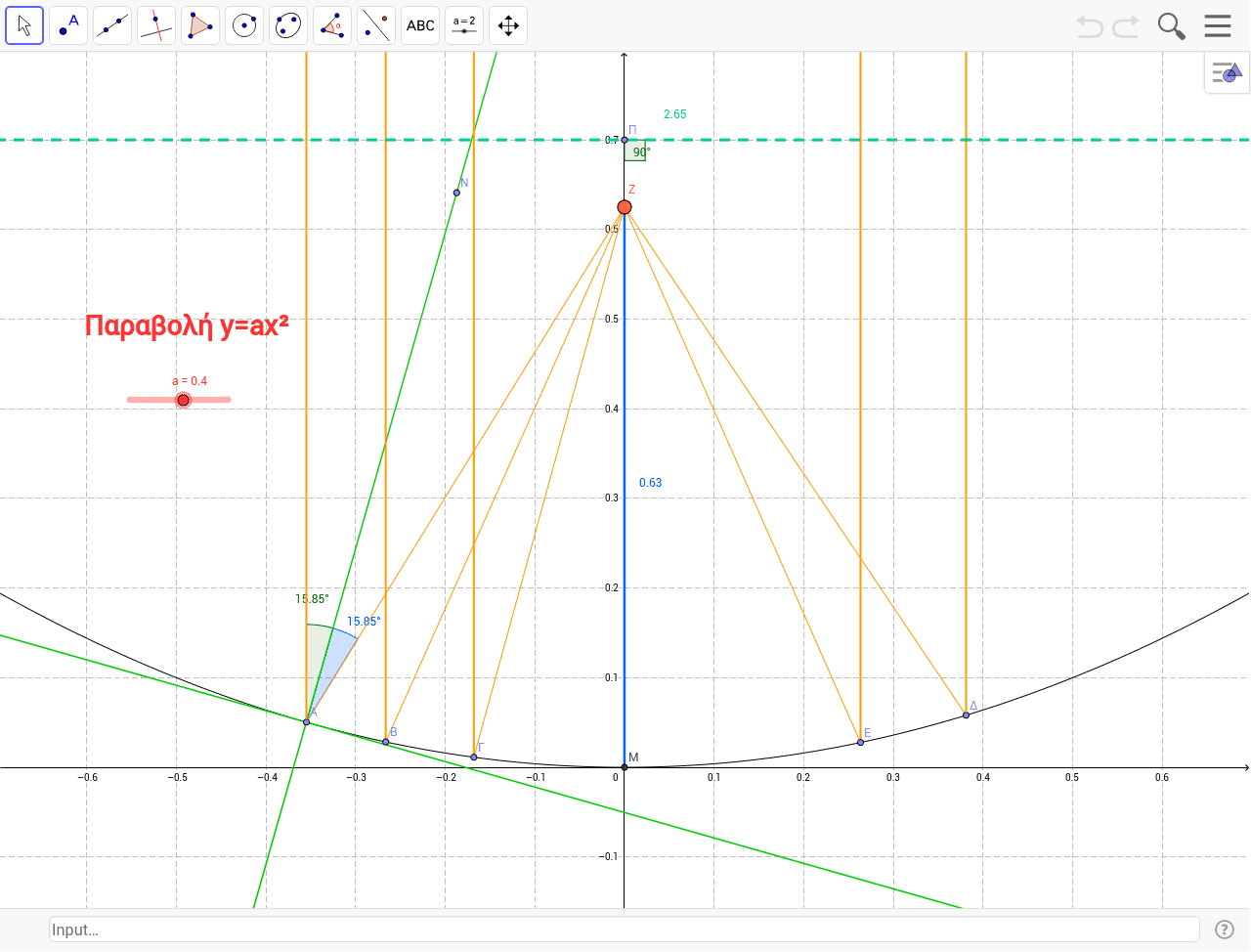


Parabola Y Ax 2 Geogebra


Sat Math Multiple Choice Question 2 Answer And Explanation Cracksat Net
By translating the parabola x 2 = 2py its vertex is moved from the origin to the point A (x 0, y 0) so that its equation transforms to (xx 0) 2 = 2p(yy 0) The axis of symmetry of this parabola is parallel to the yaxis As we already mentioned, this parabola is a function that we usually writeA parabola is a curve where any point is at an equal distance from a fixed point (called the focus), and a fixed straight line (called the directrix) There are two form of Parabola Equation Standard Form and Vertex Form Standard Form y = ax 2 bx c Vertex Form y = a(x h) 2 k The Vertex of the Parabola The vertex is a point V(h,k) on0 votes 1 answer If sinϴ and cosϴ roots of the quadratic equation ax2bxc=0,prove that a2b22ac=0


Quadratics
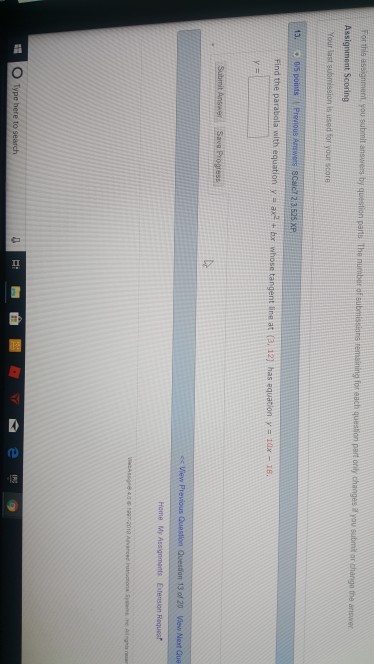


Solved Find The Parabola With Equation Y Ax 2 Bx Whose T Chegg Com
Carefully observe the equation, the negative sign indicates that the parabola will actually face downward and the vertex will be the maxima of the function Thus, the parabola has a maximum value at y = 2 and it can go down as low as it wants The range of parabola y ≤ 2 The summary of the domain and range of a parabola is the followingThis calculator will find either the equation of the parabola from the given parameters or the axis of symmetry, eccentricity, latus rectum, length of the latus rectum, focus, vertex, directrix, focal parameter, xintercepts, yintercepts of the entered parabola To graph a parabola, visit the parabola grapher (choose the "Implicit" option)Do you think the rate of change will be the same at every point on the parabola?


Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola


Examining The Parabola Assignment 2
# slope # (dy/dx)=4# Plug in these values #2a(1)b=4# #2ab=4#(1)So there is a fundamental question here how can we translate a standard parabola to get the general parabola \(\normalsize{y=ax^2bxc}\)?Free Parabola calculator Calculate parabola foci, vertices, axis and directrix stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy
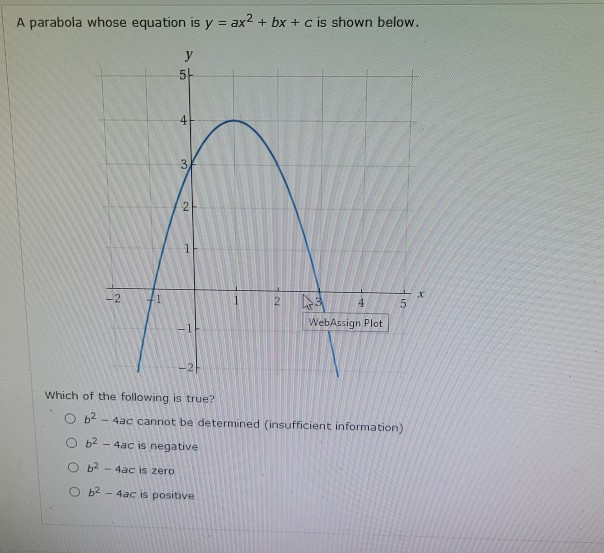


Solved A Parabola Whose Equation Is Y Ax2 Bx C Is S Chegg Com


Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola
Write the equation of the parabola y=ax^2bxc that passes through the points(0,3), (1,4), and (2,3) College Algebra Find the standard form of the equation of the parabola with the given characteristics and vertex at the origin Passes through the point (5, 1/8);User The line of symmetry of the parabola whose equation is y = ax^2 4x 3 is x = 2What is the value of "a"?Show your work A line is tangent to a curve if it only touches it in one point mathax^2x=3x1/math math\implies ax^22x1=0/math math



The Parabola Y Ax 2 Bx C Is Graphed Below Find A B C The Grid Lines Are One Unit Brainly Com


Quadratics
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How YouTube works Test new features Press Copyright Contact us CreatorsKnow the equation of a parabola The general equation of a parabola is y = ax 2 bx cIt can also be written in the even more general form y = a(x – h)² k, but we will focus here on the first form of the equation If the coefficient a in the equation is positive, the parabola opens upward (in a vertically oriented parabola), like the letter "U", and its vertex is a minimum pointSince a parabola \(\normalsize{y=ax^2bxc}\) is specified by three numbers, it is reasonable to suppose that we could fit a parabola to three points in the plane This is indeed the case, and it is a useful idea In this step we see how to algebraically fit a parabola to three points in the Cartesian plane This involves recalling, or learning


If Y Ax 2 Bx C Represents A Parabola With Vertex A As Shown In The Figure And B 2 2 B 2ac Sarthaks Econnect Largest Online Education Community


Parabolas
Assuming all parabolas are of the form y = ax^2 bx c, drag and drop the graphs to match the appropriate avalue?The equation of the parabola, with vertical axis of symmetry, has the form y = a x 2 b x c or in vertex form y = a(x h) 2 k where the vertex is at the point (h , k) In this case it is tangent to a horizontal line y = 3 at x = 2 which means that its vertex is at the point (h , k) = (2 , 3) Hence the equation of this parabola may beSuppose we have a parabola y = a x 2 b x c y = ax^2 bx c y = a x 2 b x c Then the equation a x 2 b x c = 0 ax^2 bx c = 0 a x 2 b x c = 0 is bound to have two roots since it is a quadratic equation However, the number of real roots depends on the parabola


Untitled Document
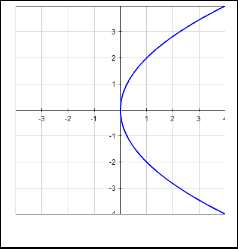


A Parabola Symmetrical To Y X Line
The Parabola Given a quadratic function \(f(x) = ax^2bxc\), it is described by its curve \y = ax^2bxc\ This type of curve is known as a parabolaA typical parabola is shown here Parabola, with equation \(y=x^24x5\)Previously, we have studied rates of change In what context have we explored the change in y in relation to the change in x before?We learn how to find the equation of a parabola by writing it in vertex form In the previous section, we learnt how to write a parabola in its vertex form and saw that a parabola's equation \y = ax^2bxc\ could be rewritten in vertex form \y = a\begin{pmatrix}x h \end{pmatrix}^2k\ where \(h\) is the horizontal coordinate of the vertex


Lesson 10 2 Quadratic Functions And Their Graphs Y Ax 2 Bx C Ppt Download


The Function F X Y And Associated Matrices E And E
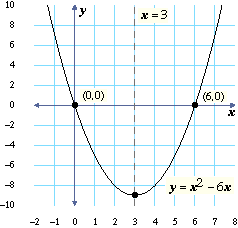
0 $$ it opens downwards The axis of symmetry The axis of symmetry is the line $$ x = \frac{b}{2a} $$Im sorry for number 3 its The xintercepts of the parabola y=x^2bx are (3,0) and (5,0) Find the equation of the parabola, and submit your answer in y=ax^2bxc form The x coordinate of vertex will occur halfway between the x intercepts = (5 3) /2 = 1 And the x coordinate of the vertex = b / (2a) where a = 1 SoHttp//wwwlezionidimateit http//wwwwikimateit In questa lezione cominciamo a definire la parabola e successivamente trattiamo il caso specifico di una p


Investigating Y Ax 2 Bx


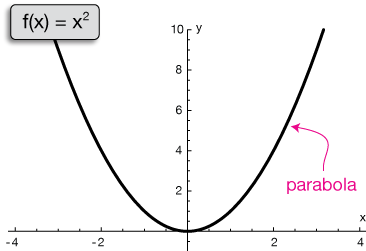
Intro To Quadratic Graphs Key Features Of Parabolas Expii
The standard equation of a parabola is given by y= ax2bxc y = a x 2 b x c where a and b are constants, and c is a constant representing the yintercept The xcoordinate of the vertex isThe standard form of a parabola's equation is generally expressed $ y = ax^2 bx c $ The role of 'a' If $$ a > 0 $$, the parabola opens upwards ;If $$ a ;


Quadratic Graph Example Y Ax Expii


Quadratic Function Y Ax2 Bx C When A Is Sutori
The directrix of a parabola is the horizontal line found by subtracting from the ycoordinate of the vertex if the parabola opens up or down Substitute the known values of and into the formula and simplify Use the properties of the parabola to analyze and graph the parabola Direction Opens Down VertexFree Parabola calculator Calculate parabola foci, vertices, axis and directrix stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie PolicyLet the equation of the parabola be #y=ax^2bxc# We have to find the values of the parameters #a, b and c# to fix the equation Its slope #(dy/dx)# of the function #y=ax^2bxc# is defined by its first derivative #dy/dx=2axb# Then, at #x=1;



Graphing A Parabola Of The Form Y Ax2 Bx C With Rational Coefficients Youtube



Quadratic Function
Parabola is a mirrorsymmetrical, plane curve and typically Ushaped A parabola is a curve where any point is at an equal distance from Fixed Point (the focus) A fixed straight line (the directrix) There are two forms of Parabola Standard Form The standard equation of Parabola is y=ax 2 bxcIf $$ a ;Hi evinda, The parametrization $(at^2, t)$, $t\in \b R$, is not a parametrization of the parabola $y = ax^2$, but rather the parabola $x = ay^2$
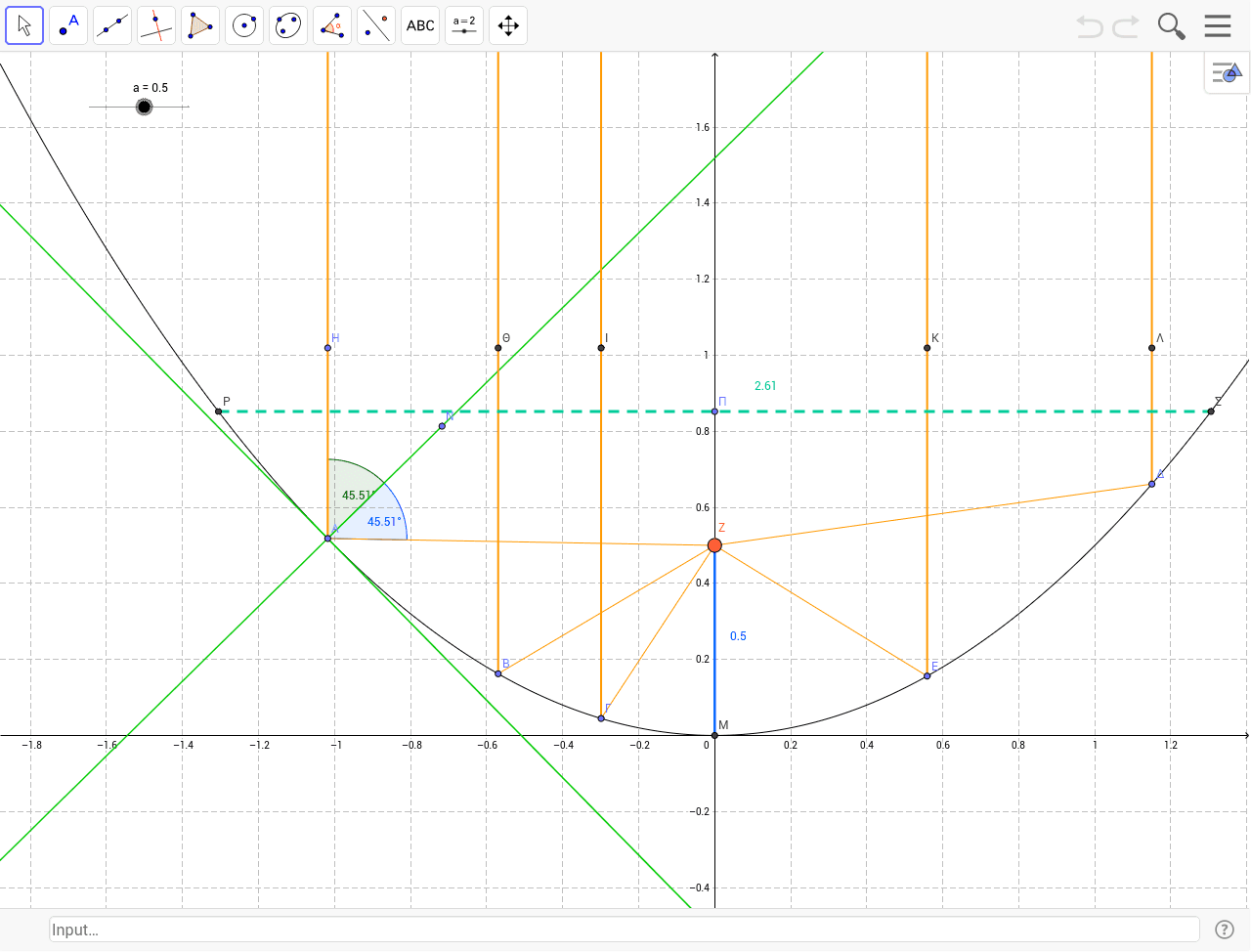


Parabola Y Ax 2 Geogebra



The Parabola Maths Grade 10 Rought Draft Openstax Cnx
Example 11Find the area of the parabola 𝑦2=4𝑎𝑥 bounded by its latus rectumFor Parabola 𝑦2=4 𝑎𝑥Latus rectum is line 𝑥=𝑎Area required = Area OLSL' =2 × Area OSL = 2 × 0𝑎𝑦 𝑑𝑥𝑦 → Parabola equation 𝑦2=4 𝑎𝑥 𝑦=± 4 𝑎𝑥Since OSL is in 1st quadrantPreviously, we have studied rates of change In what context have we explored the change in y in relation to the change in x before?> What is the equation y=ax^2 x of the parabola that is tangent to the line with equation y=3x1?


Quadratics Terms Sparknotes


Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola
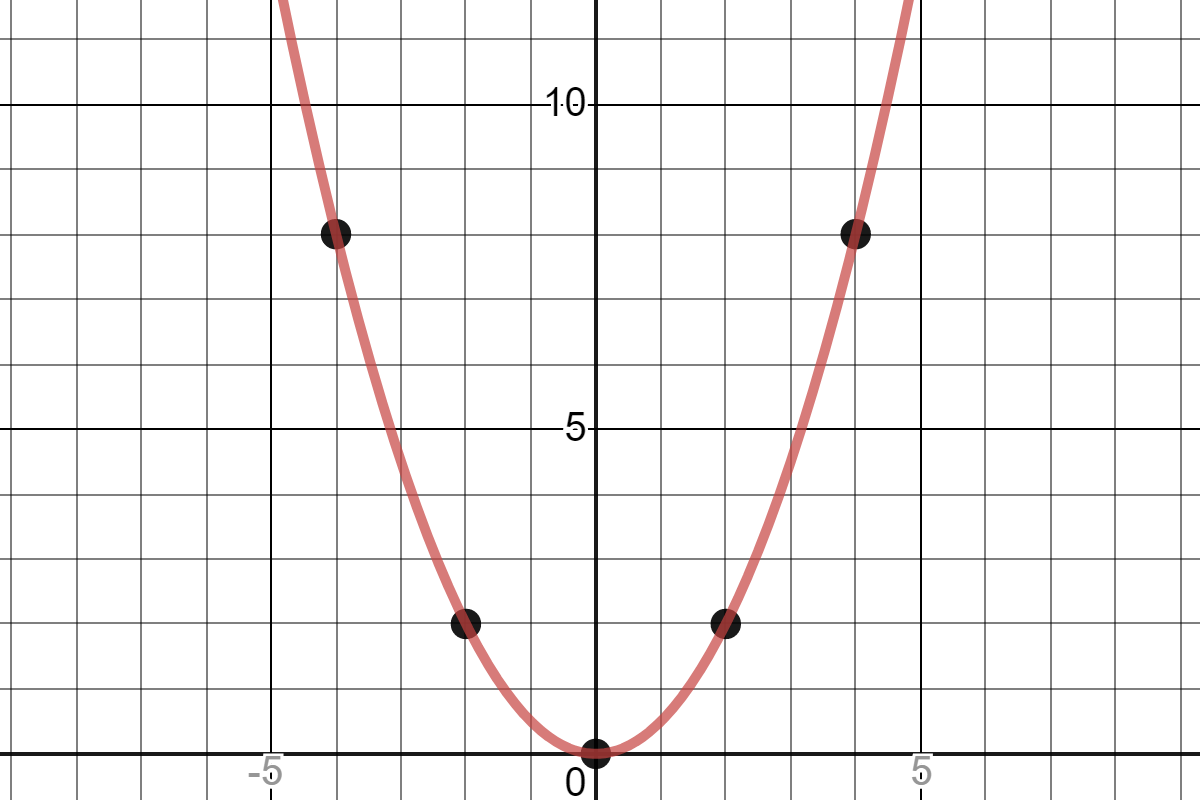
That means that the points on the parabola, when plugged into the equation, make a true statement, and conversely, the only points that can be plugged in to make the equation true are points on the parabolaYou can put this solution on YOUR website!Find a and k so that the parabola y=ax^2 k passes through the points (3,11) and (4,18) Show all steps please ) ANSWER y=x^2 2


Quadratic Graph Example Y Ax Expii


Topic U2 L1 Parts Of A Quadratic Function Graphing Quadratics Y Ax 2 Bx C Eq Can I Identify The Vertex Axis Of Symmetry X And Y Intercepts Ppt Download
Hi evinda, The parametrization $(at^2, t)$, $t\in \b R$, is not a parametrization of the parabola $y = ax^2$, but rather the parabola $x = ay^2$A > 0 parabola opens up minimum value a < 0 parabola opens down maximum value A rule of thumb reminds us that when we have a positive symbol before x 2 we get a happy expression on the graph and a negative symbol renders a sad expressionThe general form of a quadratic is "y = ax 2 bx c"For graphing, the leading coefficient "a" indicates how "fat" or how "skinny" the parabola will beFor a > 1 (such as a = 3 or a = –4), the parabola will be "skinny", because it grows more quickly (three times as fast or four times as fast, respectively, in the case of our sample values
%20of%20a%20parabola%201.gif)


Finding The Y Intercepts Of A Parabola


Parabolas
Write the equation of the parabola y=ax^2bxc that passes through the points(0,3), (1,4), and (2,3) College Algebra Find the standard form of the equation of the parabola with the given characteristics and vertex at the origin Passes through the point (5, 1/8);Corresponding parabola or quadratic function y = ax^2 bx c Solutions are xintercepts of this parabola • The solution is Simplify and write as 2 separate numbers if b^2 − 4ac is a perfect squareThe parabola passes through the points (1,3) and (3,13) find the values of a and k Equation 1 Equation 2 Subtract the 1st equation from the 2nd equation, the result is, divide both sides by 8 a = 2, substitute into Equation 1 and solve for k


The Department Of Mathematics Education J Wilson Emat 6680 Assignment 2 Quadratics By Hulya Kilic In This Assignment I First Constructed The Graphs Of Parabolas Having Standard Form Y Ax2 Bx C Here The Graphs Of The Parabolas That I Chose Then
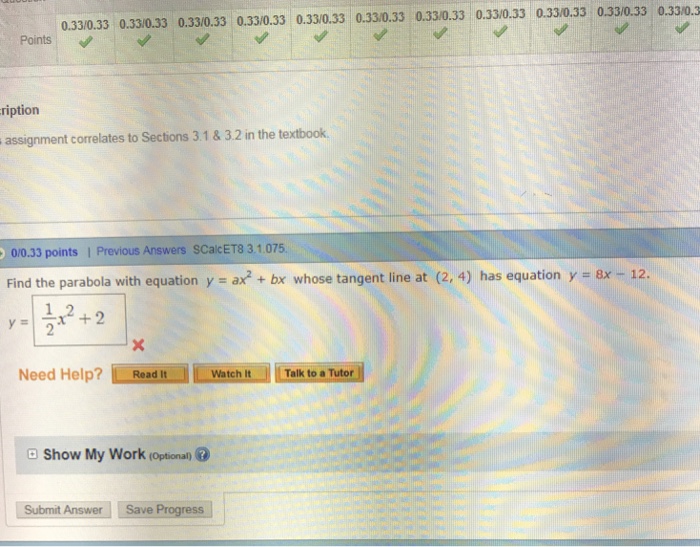


Solved Find The Parabola With Equation Y Ax 2 Bx Whos Chegg Com
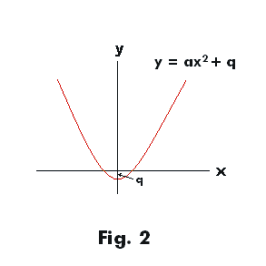
In mathematics, a parabola is a plane curve which is mirrorsymmetrical and is approximately UshapedIt fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves One description of a parabola involves a point (the focus) and a line (the directrix)The focus does not lie on the directrix The parabola is the locus of points inSuppose we have a parabola y = a x 2 b x c y = ax^2 bx c y = a x 2 b x c Then the equation a x 2 b x c = 0 ax^2 bx c = 0 a x 2 b x c = 0 is bound to have two roots since it is a quadratic equation However, the number of real roots depends on the parabolaY = ax 2 c, where a≠ 0 In the parent function, y = x 2, a = 1 (because the coefficient of x is 1) When the a is no longer 1, the parabola will open wider, open more narrow, or flip 180 degrees Examples of Quadratic Functions where a ≠ 1


The Graph Of Y Ax 2 Bx C Has A Minimum At 5 3 And Passes Through 4 0 How Do I Find The Values Of A B And C Quora


Ppt Standard Form Of Quadratic Function Y Ax 2 Bx C Powerpoint Presentation Id
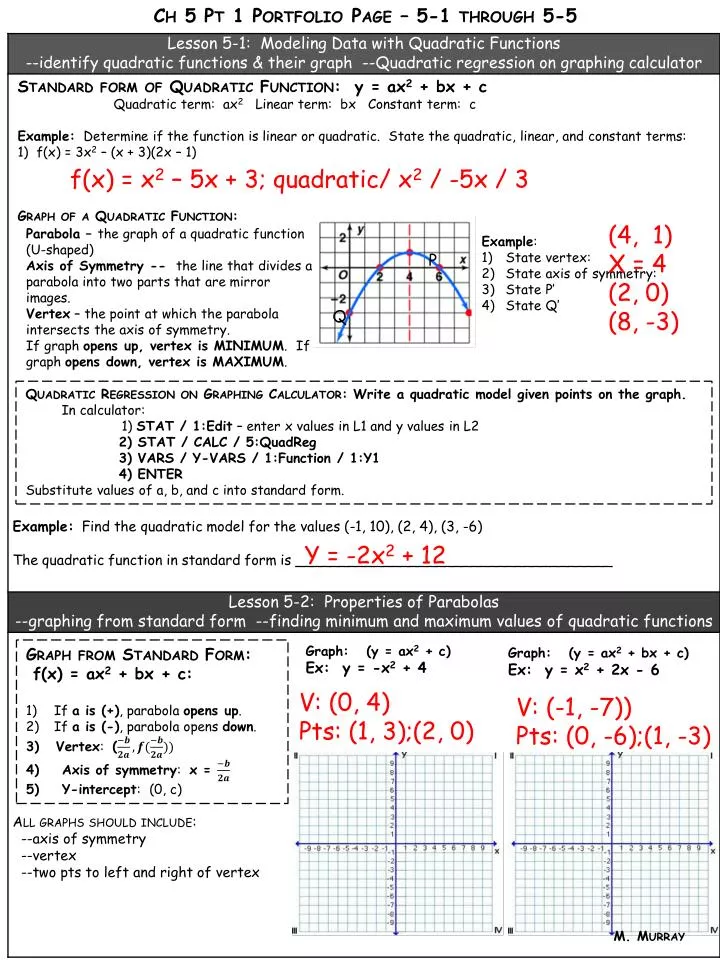
Finding the answer will take us to ancient Persia, to a technique called completing the square, and to a remarkable identity that all students of mathematics ought to have seenGiven a function of the form y = ax^2 where a is negative, where is the function increasing and where is it decreasing?PARABOLAS TRANSLATIONS AND APPLICATIONS QUADRATIC RELATION A quadratic relation in two variables is a relation that can be written in the form y=ax^2bxc or x=ay^2byc where a, b, and c are real numbers, and a!=0 The graphs of quadratic relations are called parabolas The simplest quadratic relation of the form y=ax^2bxc is y=x^2, with a=1, b=0, and c=0, so this relation is graphed first



Axis Of Symmetry Of A Parabola
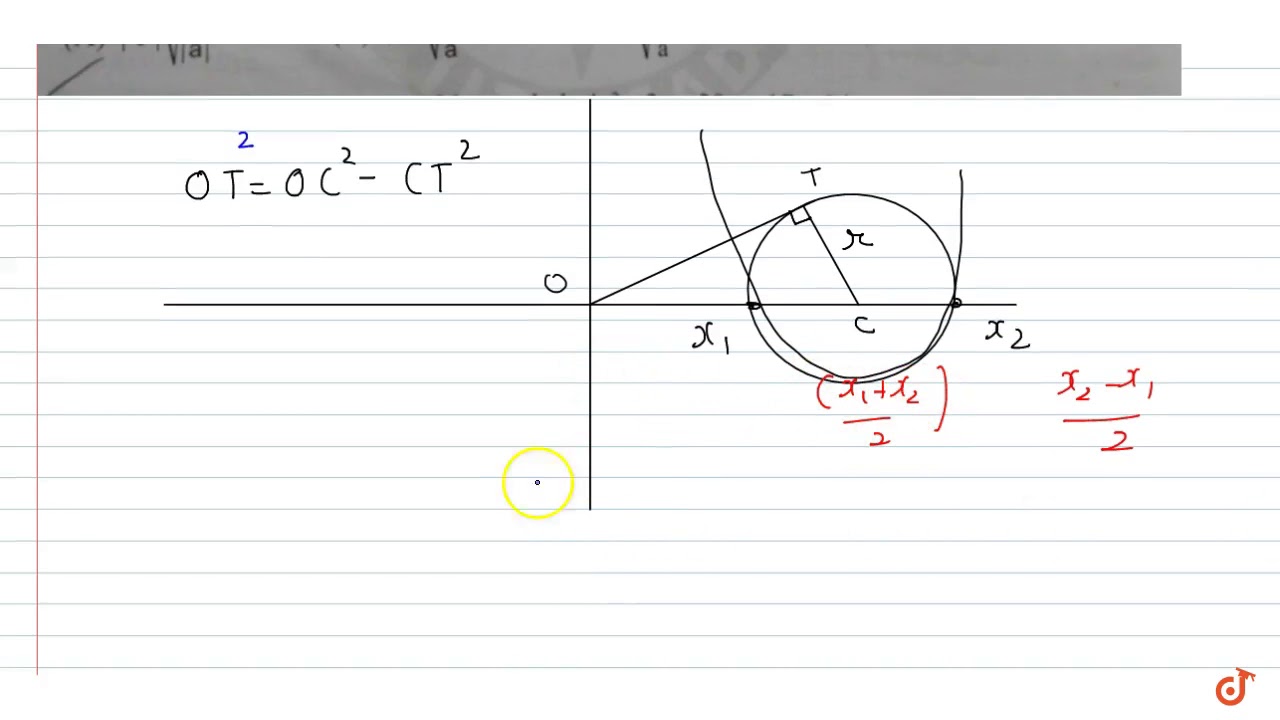


A Parabola Y Ax 2 Bx C Ac Gt 0 Crosses The X Axis At A And B A Variable Circle Is Dra Youtube
Given a function of the form y = ax^2 where a is negative, where is the function increasing and where is it decreasing?Exploring Parabolas by Kristina Dunbar, UGA Explorations of the graph y = ax 2 bx c In this exercise, we will be exploring parabolic graphs of the form y = ax 2 bx c, where a, b, and c are rational numbers In particular, we will examine what happens to the graph as we fix 2 of the values for a, b, or c, and vary the third We have split it up into three partsOne formula works when the parabola's equation is in vertex form and the other works when the parabola's equation is in standard form Standard Form If your equation is in the standard form $$ y = ax^2 bx c $$ , then the formula for the axis of symmetry is $ \red{ \boxed{ x = \frac {b}{ 2a} }} $ Vertex Form If your


Lessons 5


Content Transformations Of The Parabola
Graphing Parabolas Fill in the form with the values from your problem, then click "Draw it!" The form y=ax 2 y= x 2 Plot Information Color Xaxis range Minimum Maximum Yaxis range Minimum Maximum Number of points to calculate and plot Quick!Suppose a parabola y = ax^2 bx c has two x intercepts, one positive and one negative, and its vertex is (2, –2) asked May 3, 19 in Mathematics by RenuK (681k points) kvpy;The standard form of parabola is given by {eq}y = ax^2 bx c {/eq} Since the three given noncollinear points {eq}\left( 0, 5 \right) \, , \, \left( 3, 2 \right) \, \text{and} \, \left( 2, 13
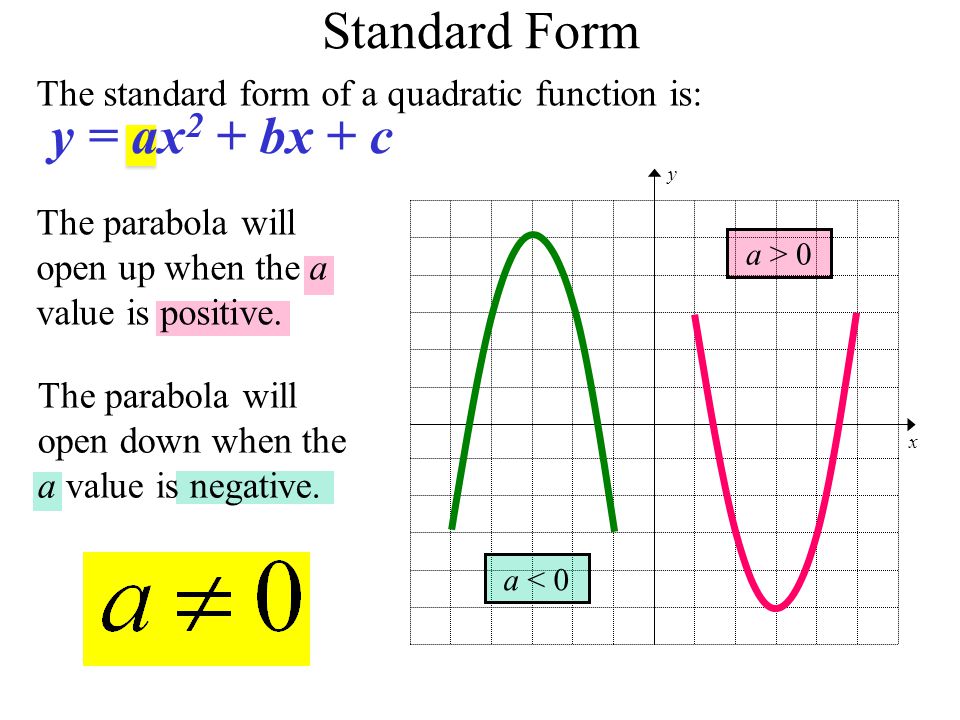


Graphing Quadratic Functions Ppt Video Online Download


Examining The Parabola Assignment 2
The graph of a quadratic function is a parabola The parabola can either be in "legs up" or "legs down" orientation We know that a quadratic equation will be in the form y = ax 2 bx c


K10outline Parabola



Graphing With The Vertex Form Of Quadratic Functions Read Algebra Ck 12 Foundation


Vertex Form How To Find The Equation Of A Parabola


Lessons 5
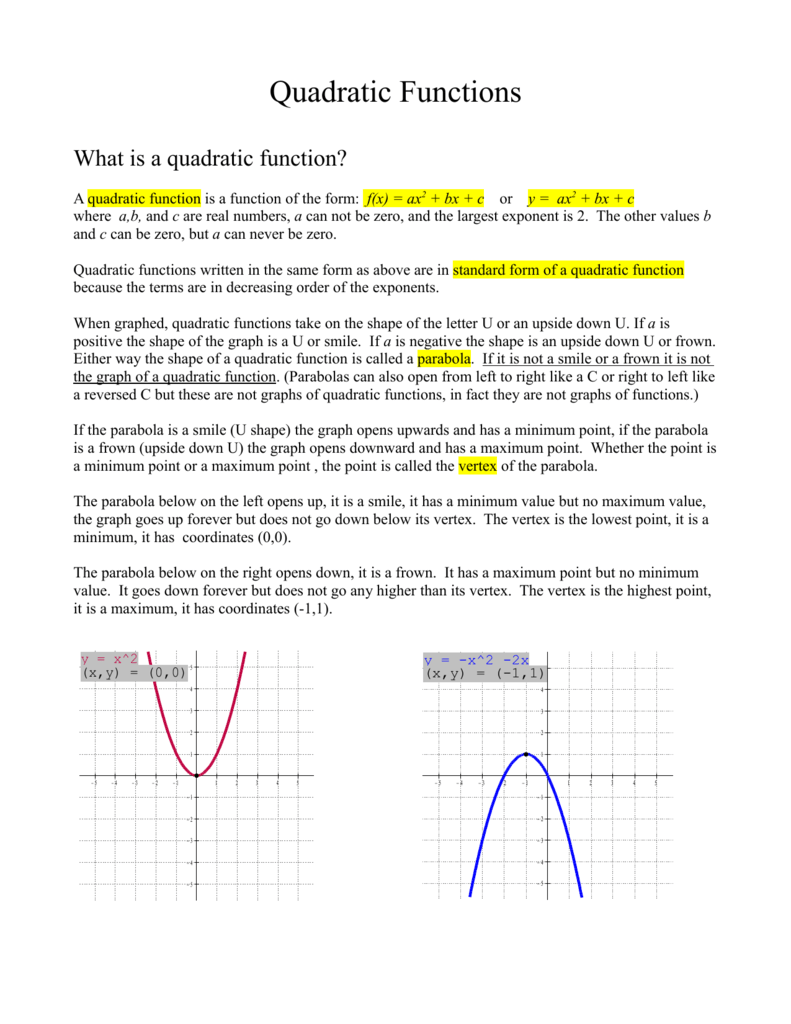


Quadratic Functions
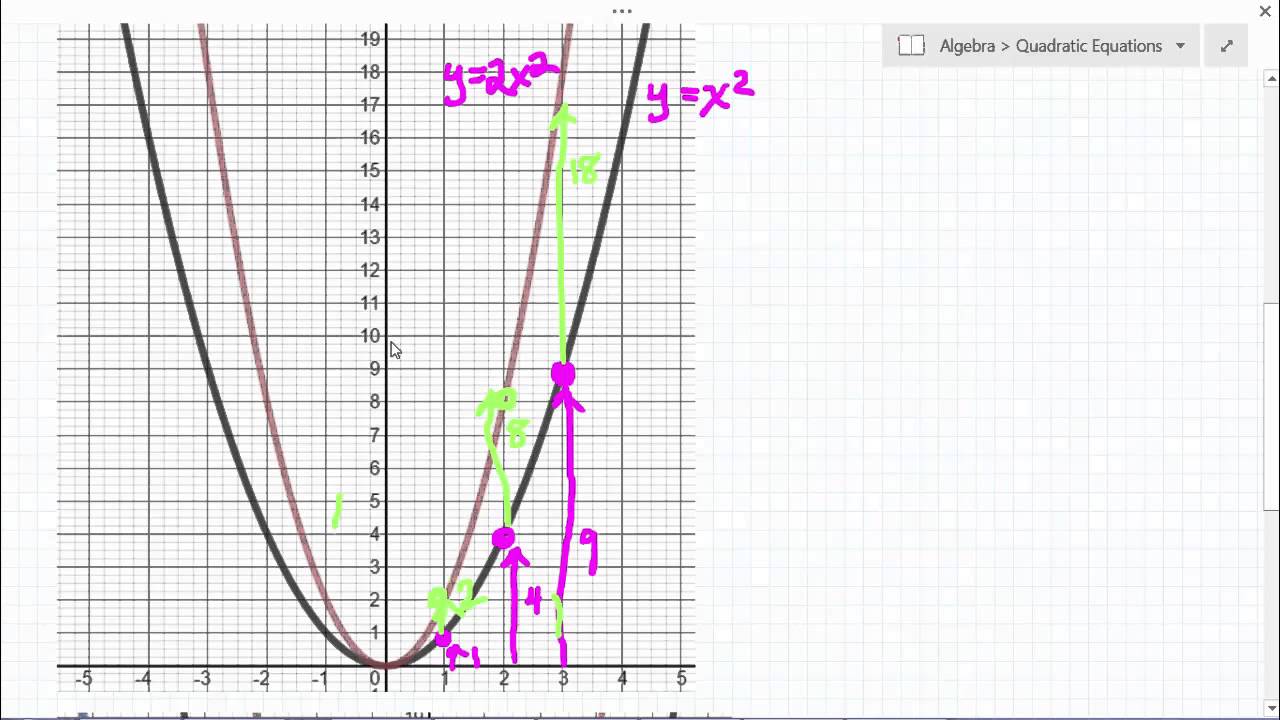


Graphing Parabola Y Ax 2 Youtube
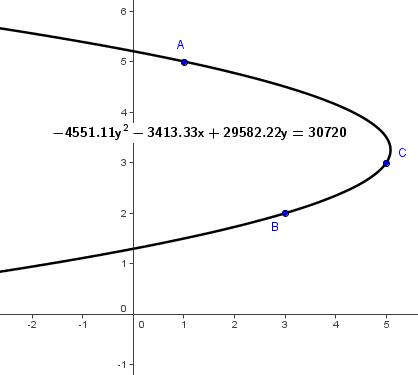


How To Find The Equation Of A Quadratic Function From Its Graph
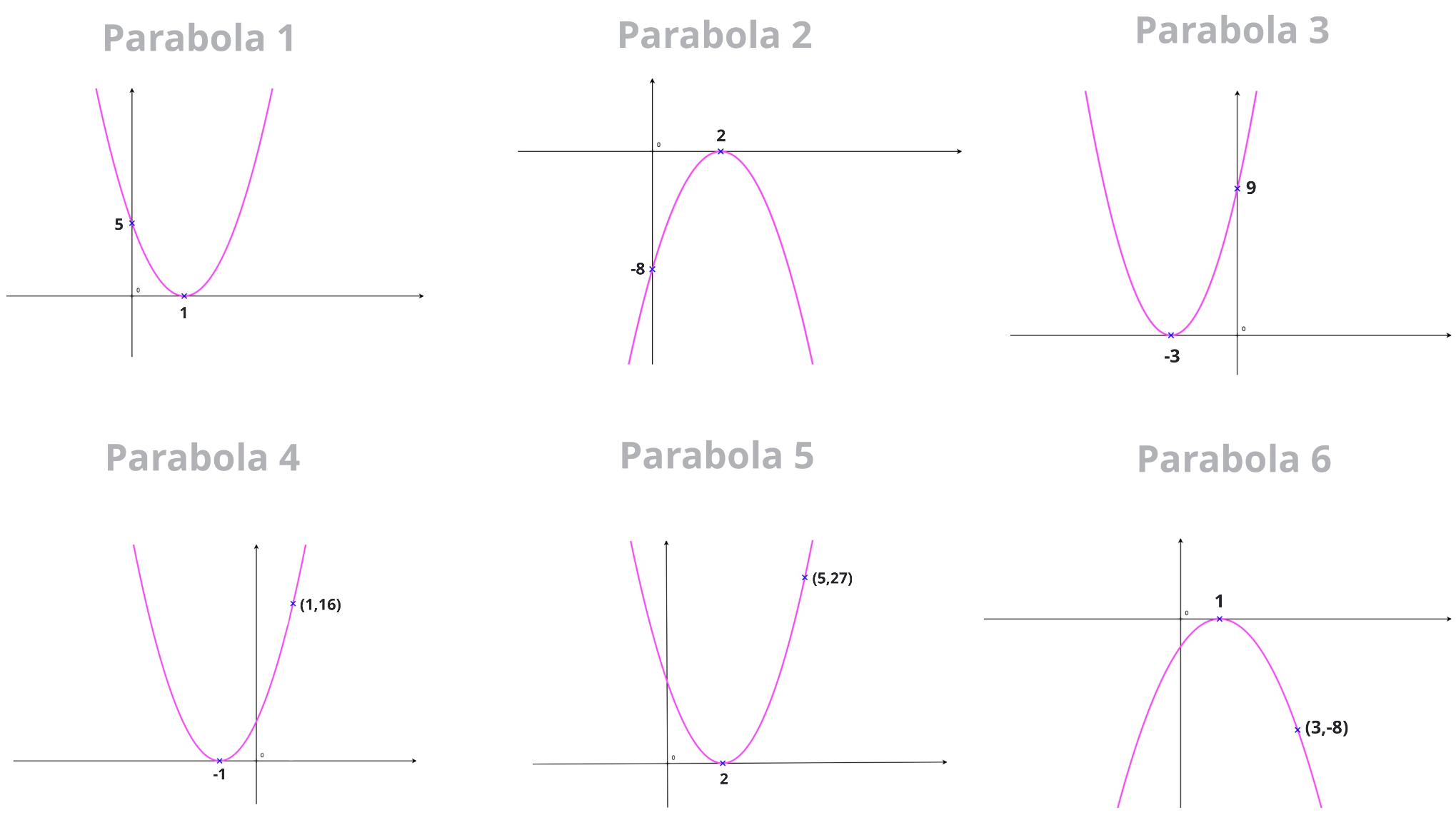


Root Factoring Quadratics How To Find The Equation Of A Parabola



Graphing Parabolas



Graphing Quadratic Functions Y Ax 2 Bx C Graphing Quadratic Functions Today We Will Understand How The Coefficients Of A Quadratic Function Influence Ppt Download


Quadratics


To Investigate The Effect Of The Constants A B And C On The Graph Y Ax2 Bx C Gcse Maths Marked By Teachers Com
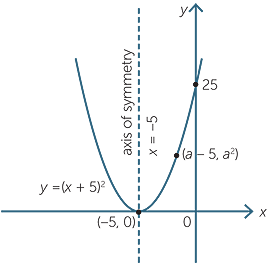


Quadratic Function


What Is The Equation Y Ax 2 X Of The Parabola That Is Tangent To The Line With Equation Y 3x 1 Show Your Work Quora


How To Draw The Graph Of Y 2 Ax Quora



B Value Definition Explanation Video Lesson Transcript Study Com


Vertex Directrix And Focus Of Quadratic Equations
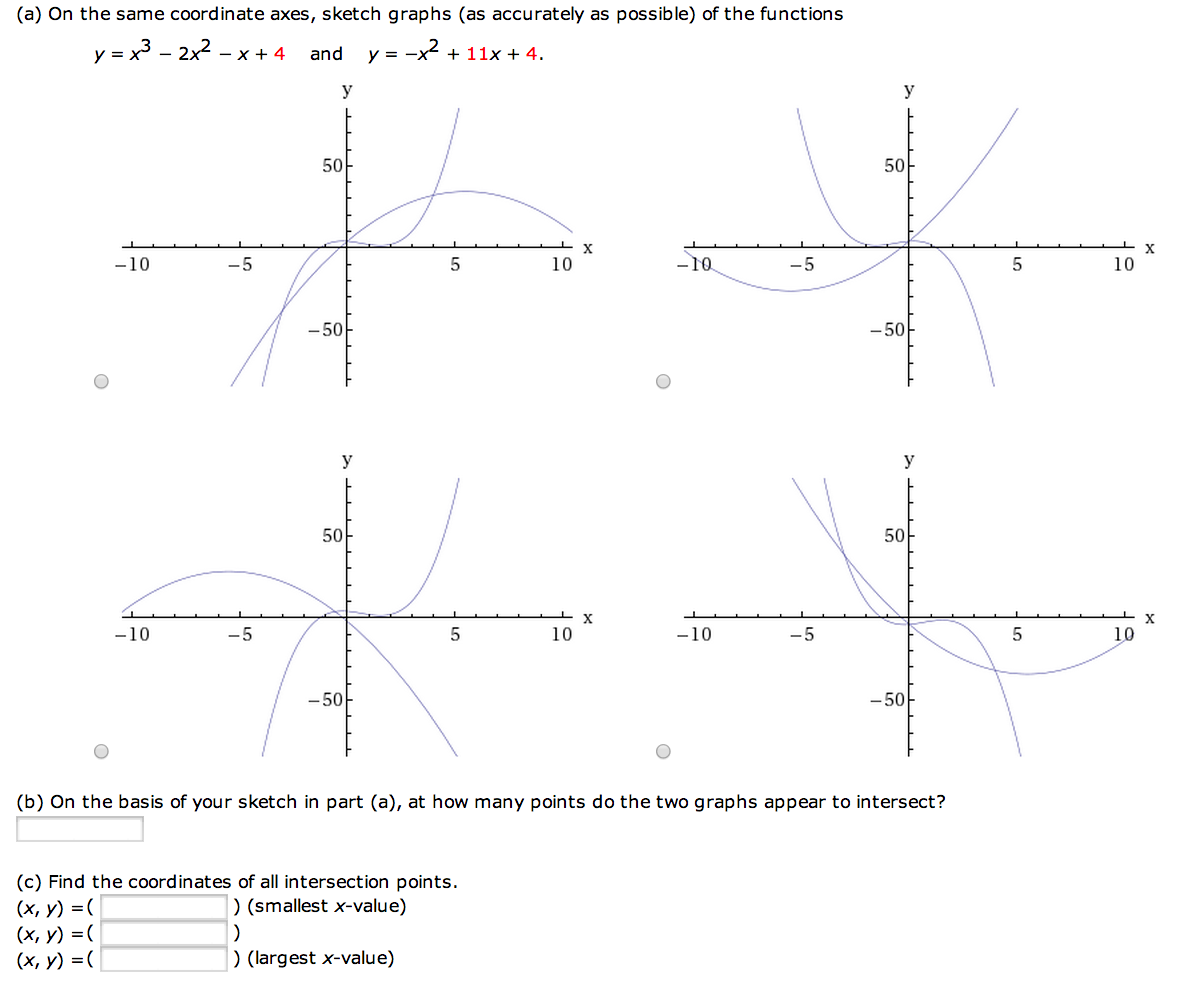


Solved Find A Parabola With Equation Y Ax2 Bx C Tha Chegg Com
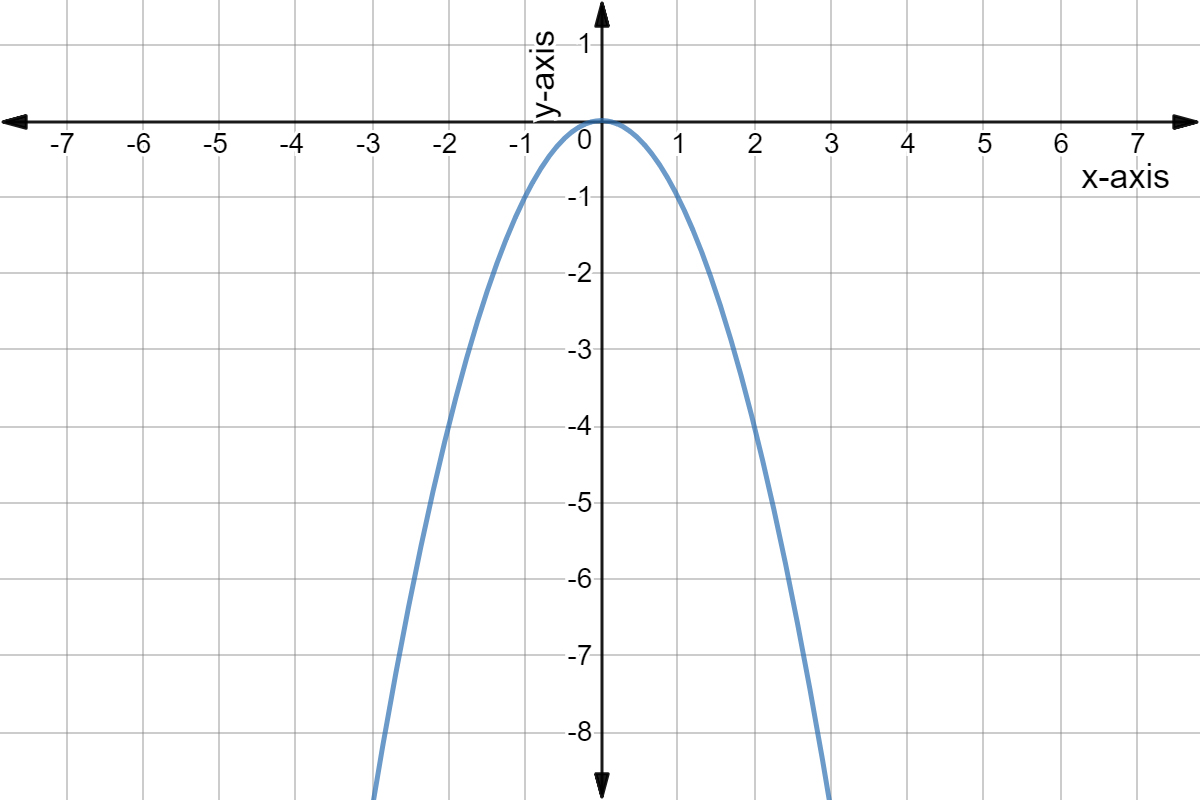


Intro To Quadratic Graphs Key Features Of Parabolas Expii


Graphing Parabolas In The Form Y Ax 2 Youtube


Ppt Recall The Graph Of A Quadratic Function Y Ax 2 Bx C Is A Parabola Powerpoint Presentation Id
/asSF.jpg)


Axis Of Symmetry Parabola


Transformations Of Equations Of Parabola Parametric Equations Of Parabola



Quadratic Function
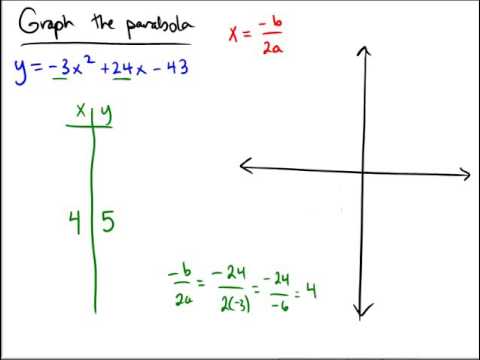


Graphing A Parabola Of The Form Y Ax 2 Bx C Integer Coefficients Youtube
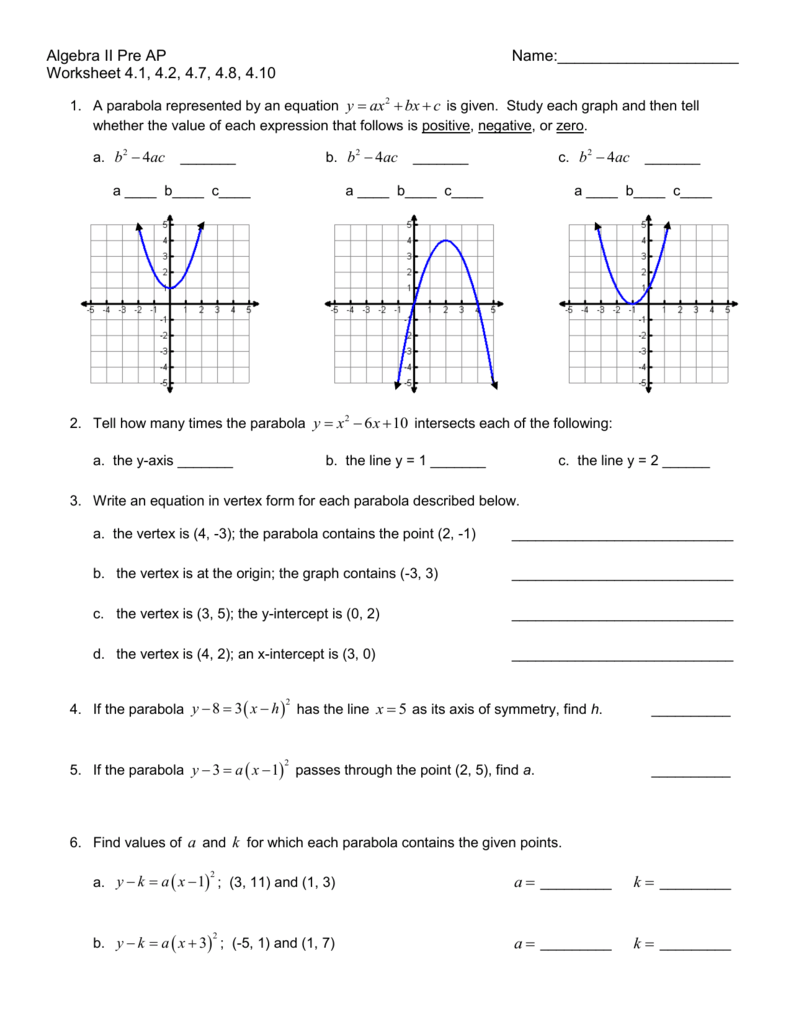


H Gt Algebra 2 Worksheet 4



Find The X Intercept And Y Intercept 1 3x 5y 15 2 Y 2x 7 Answer 5 0 0 3 Answer 0 0 7 7 2 Ppt Download



Each Member Of The Family Of Parabolas Y Ax 2 2x 3 Has A Maximum Or A Minimum Point De Youtube
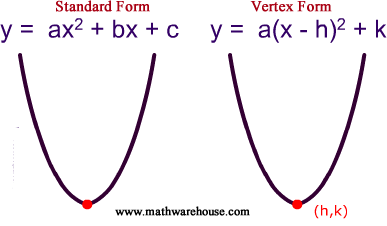


Standard And Vertex Form Of The Equation Of Parabola And How It Relates To A Parabola S Graph


All Elementary Mathematics Study Guide Functions And Graphs Elementary Functions And Their Graphs



Graphing Quadratics


Exploring Parabolas Y Ax 2 Bx C


Quadratics



Quadratic Equations Tutorial
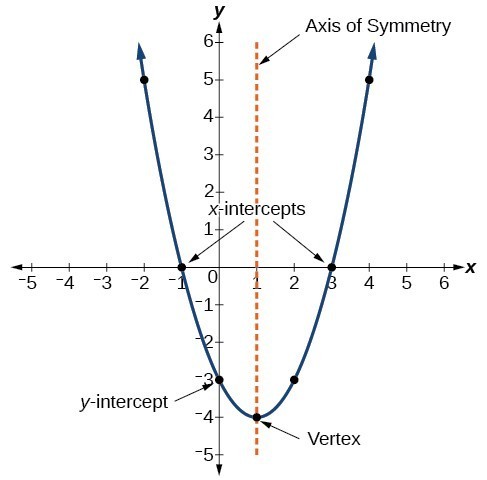


Characteristics Of Parabolas College Algebra
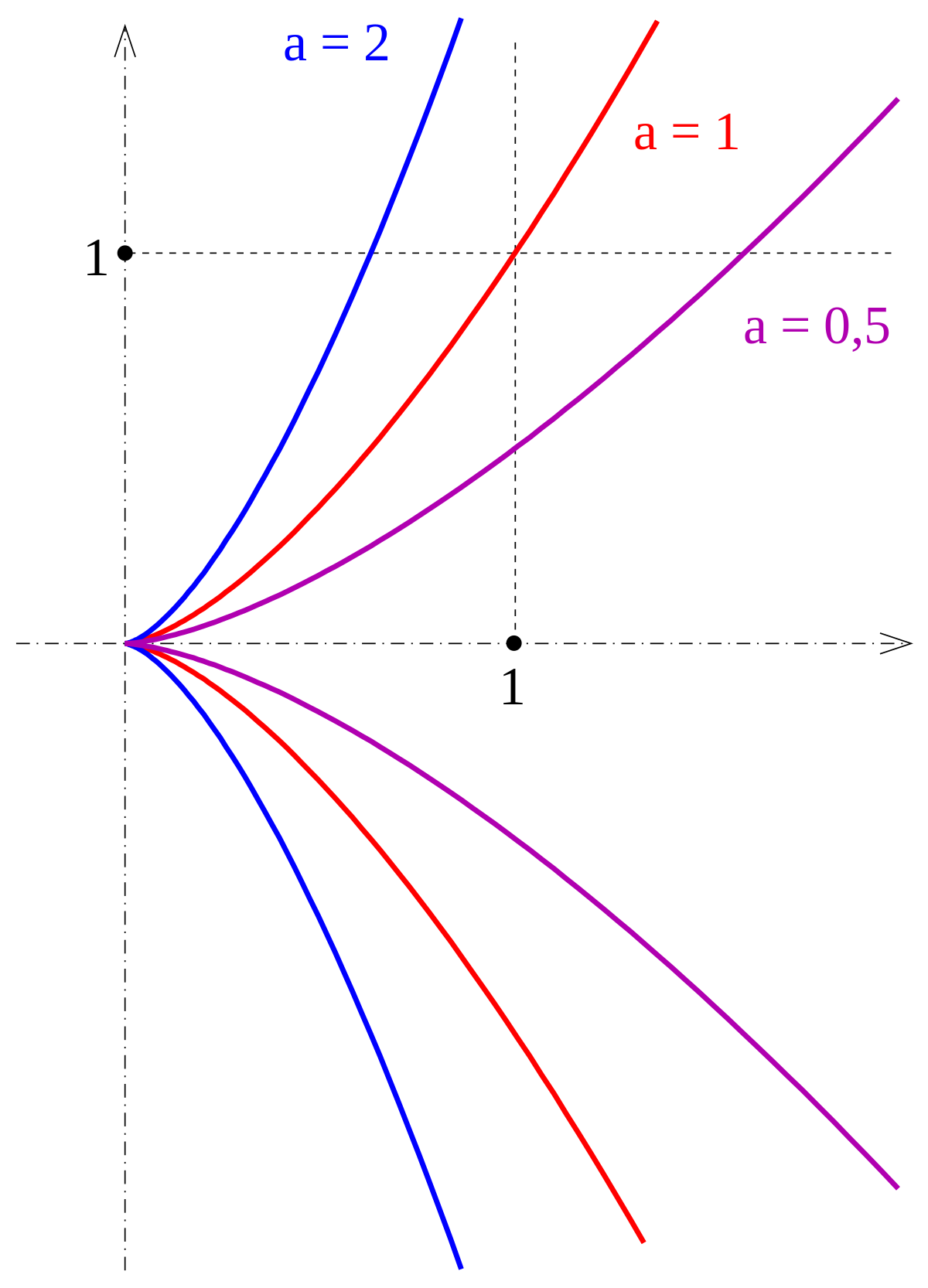


Semicubical Parabola Wikipedia


Parabola
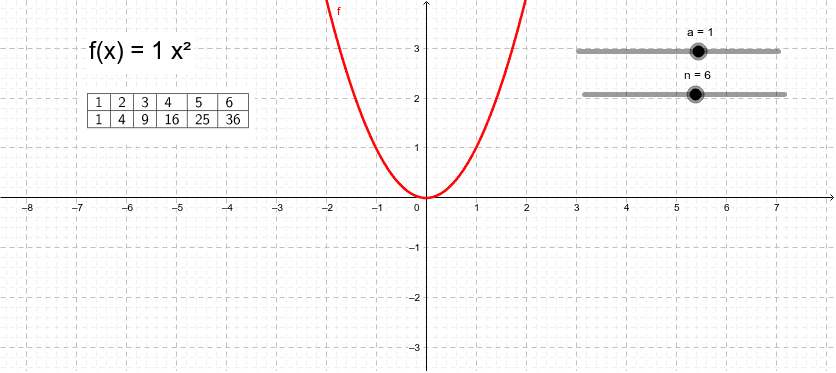


Parabola Y Ax 2 Geogebra



Quadratic Formula Calculator


We Know How To Graph The Quadratic Equation Y X2
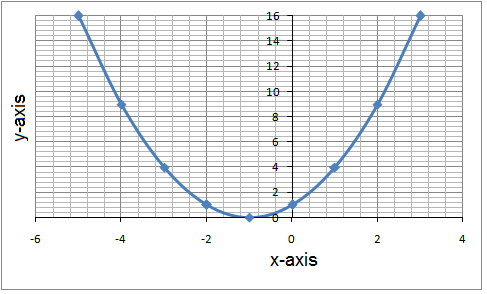


The Graph Of Y Ax 2 Bx C Algebra 1 Quadratic Equations Mathplanet



Parabola Equations And Graphs Directrix And Focus And How To Find Roots Of Quadratic Equations Quadratic Equation Quadratics Math Formulas


Sat Math Grid Ins Question 97 Answer And Explanation Cracksat Net
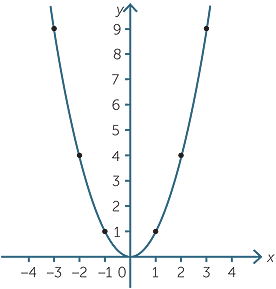


Quadratic Function
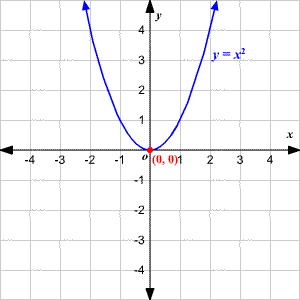


Parabolas



Quadratic Function Wikipedia



How To Find The Vertex Of A Quadratic Equation Video Lesson Transcript Study Com


Vertex And Intercepts



How To Graph A Parabola 13 Steps With Pictures Wikihow



Mfg Graphing Parabolas


Maths First Institute Of Fundamental Sciences Massey University



Characteristics Of Parabolas College Algebra
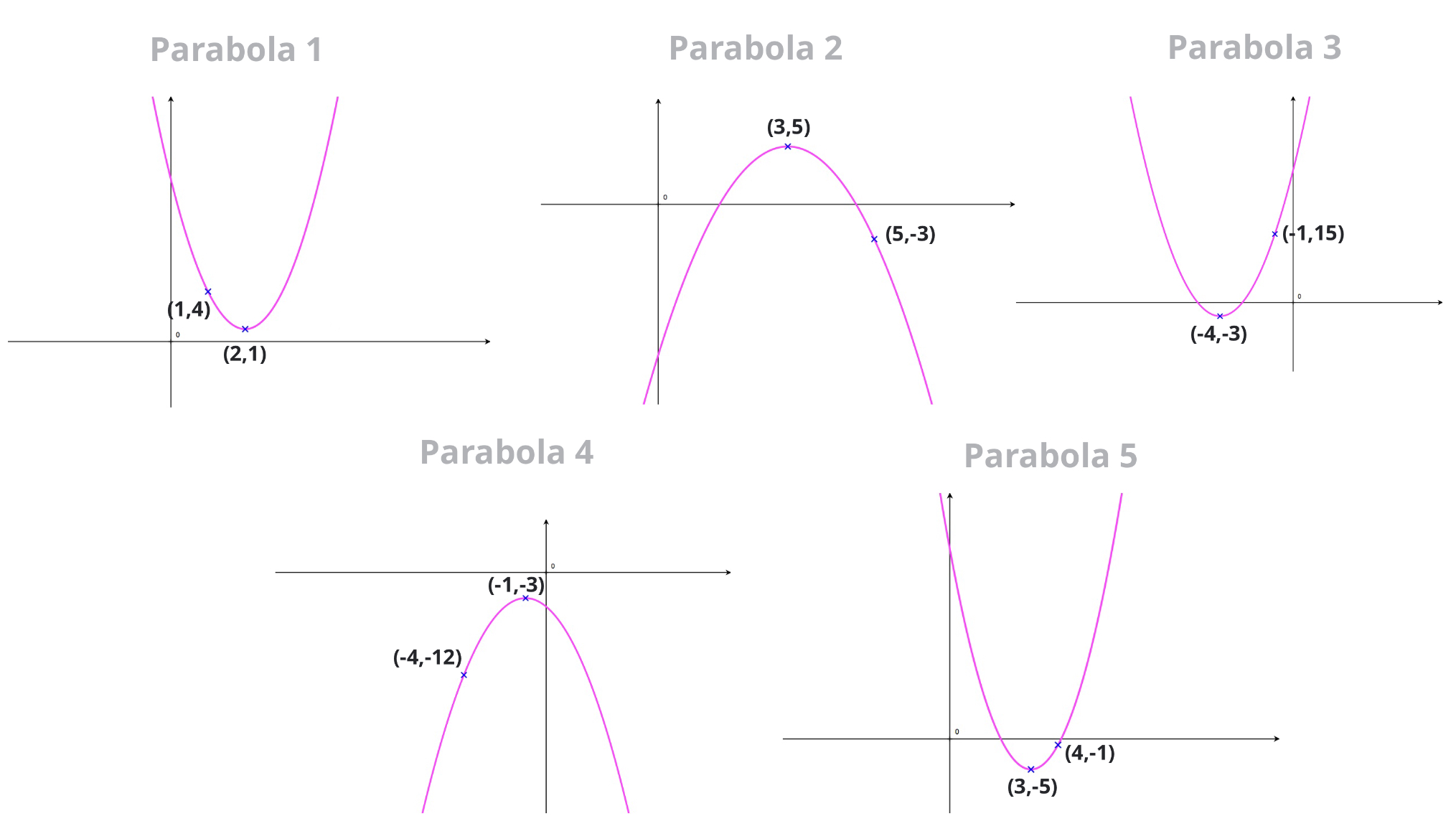


Vertex Form How To Find The Equation Of A Parabola



Quadratic Graph Example Y Ax C Expii
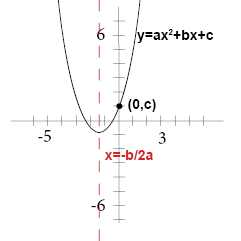


The Graph Of Y Ax 2 Bx C Algebra 1 Quadratic Equations Mathplanet
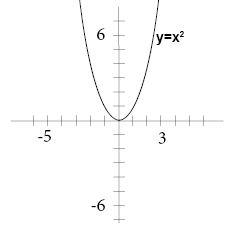


The Graph Of Y Ax 2 Bx C Algebra 1 Quadratic Equations Mathplanet


Exploring Parabolas Y Ax 2 Bx C


